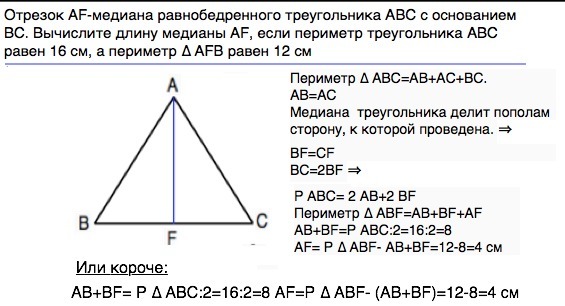
Отрезок AF-медиана равнобедренного треугольника АВС с основанием ВС. Вычислите длину медианы AF, если периметр треугольника АВС равен 16 см, А ПЕРИМЕТР ТРЕУГОЛЬНИКА AFB равен 12 см
Ответы
Ответ дал:
0
Периметр ∆ АВС=АВ+АС+ВС.
АВ=АС
Медиана треугольника делит пополам сторону, к которой проведена. ⇒
ВF=CF
ВС=2BF ⇒
P ABC= 2 AB+2 BF
Периметр АВF=AB+ВF+AF
AB+BF=P ABC:2=16:2=8
AF= P ABF- AB+BF=12-8=4 см
-------
Или короче:
АВ+ВF=P ∆ ABC:2=8
AB+BF+AF=12
AF=12-(AB+BF)=12-8=4(см)
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад