Предмет: Математика
Автор: 63hdhdndkddk74838
Вопрос задан 7 лет назад

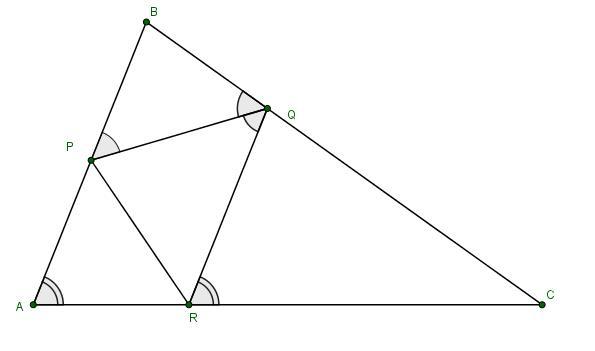
На сторонах АВ, ВС, СА треугольника АВС выбраны точки Р, Q и R соответственно так, что ВQ — ВР и АР — AR. Оказалось, биссектриса угла ВQR. Hайдите угол ARP, eсли угол QRC равен 69°. Ответ дайте в градусах.

Ответы

Ответ дал: Аноним

Задача. На сторонах АВ, ВС, СА треугольника АВС выбраны точки Р, Q и R соответственно так, что ВQ = ВР и АР = AR. Оказалось, PQ биссектриса угла ВQR. Hайдите угол ARP, eсли угол QRC равен 69°. Ответ дайте в градусах.

Решение:

Пусть $angle BQR=2alpha$ , тогда поскольку PQ - биссектриса, то $angle BQP=angle PQR=alpha$ , но по условию, PB = BQ ⇒ ΔBPQ - равнобедренный, следовательно, $angle BPQ=alpha$ , но так как $angle BPQ=angle PQR$ - накрест лежащие углы равны, то $AB parallel QR$ (первый признак параллельности прямых).

$angle CRQ=angle CAB$ как соответственные углы при AB || QR и секущей CA.

Аналогично, по условию AP = AR ⇒ ΔAPR - равнобедренный, следовательно, $angle ARP=dfrac{180^circ-angle PAR}{2}=dfrac{180^circ-69^circ}{2}=55{,}5^circ$