Помогите пожалуйста!!!! 60б ! (Задача третья с олимпиады 8 класса) Пусть АВС прямоугольный треугольник с прямым углом С , СД биссектриса треугольника , ДЕ , ДФ перпендикуляры опущенные из точки Д на стороны АС и ВС соответственно. Докажите, что ад²+бд²=(ае+бф)²
Ответы
Ответ дал:
0
Доказательство на фото
Приложения:
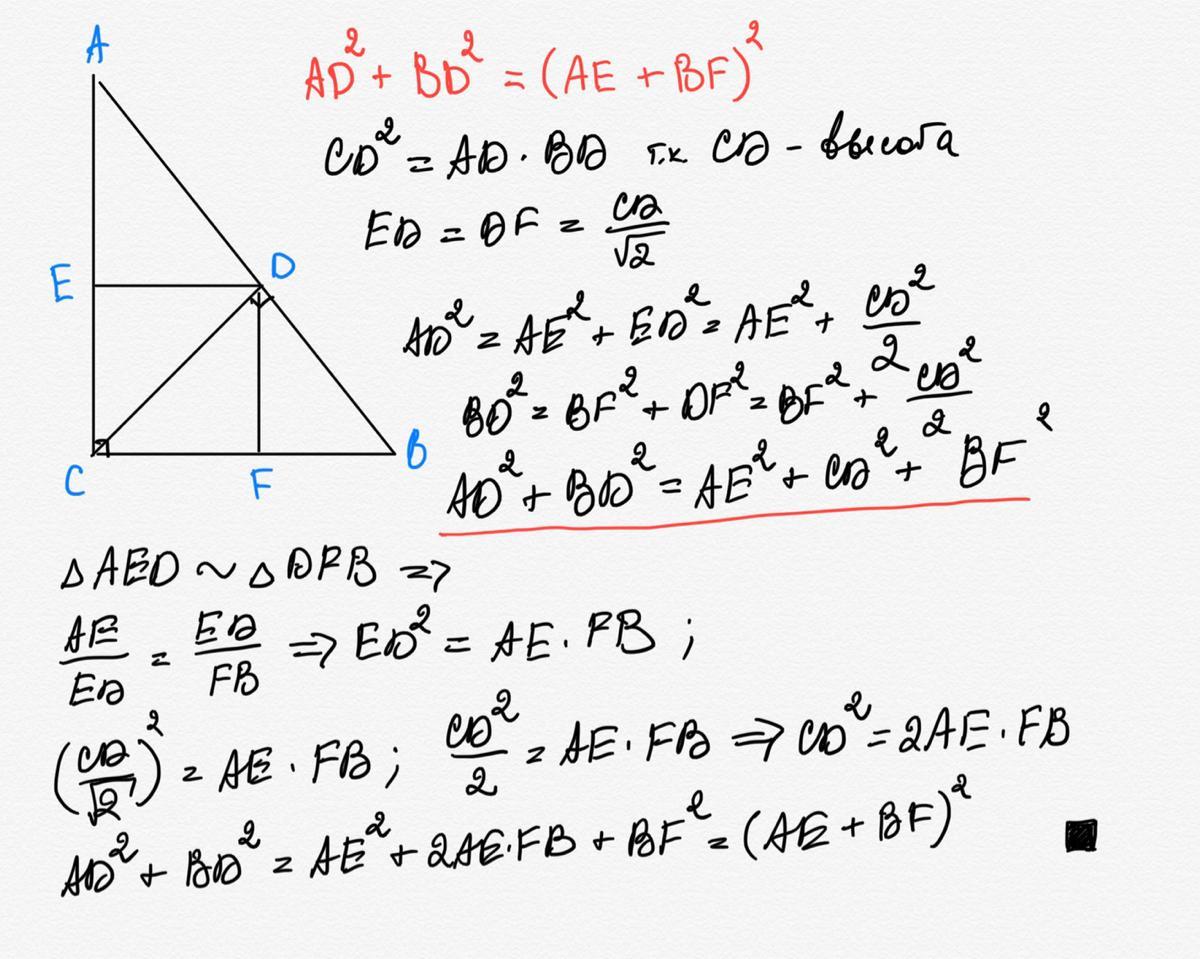
Ответ дал:
0
И они лишние
Ответ дал:
0
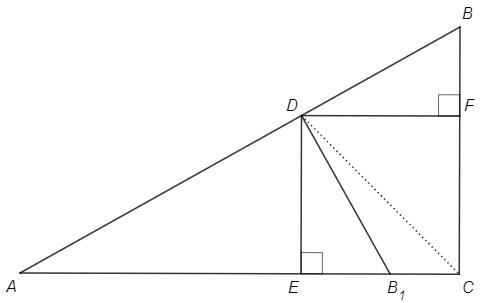
DCE =45 (CD - биссектриса)
△DEC с углами 45, 90 => равнобедренный, DE=EC
EDFC с тремя прямыми углами и равными смежными сторонами - квадрат, DE=DF
Построим B1E=BF
△B1DE=△BDF(по двум катетам) => B1D=BD, B1DE=BDF
ADE+BDF =180-90 =90
ADB1 =ADE+B1DE =ADE+BDF =90
△ADB1, по теореме Пифагора
(AE+B1E)^2 =AD^2 +B1D^2 => (AE+BF)^2 =AD^2 +BD^2
Приложения:
Похожие вопросы
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад