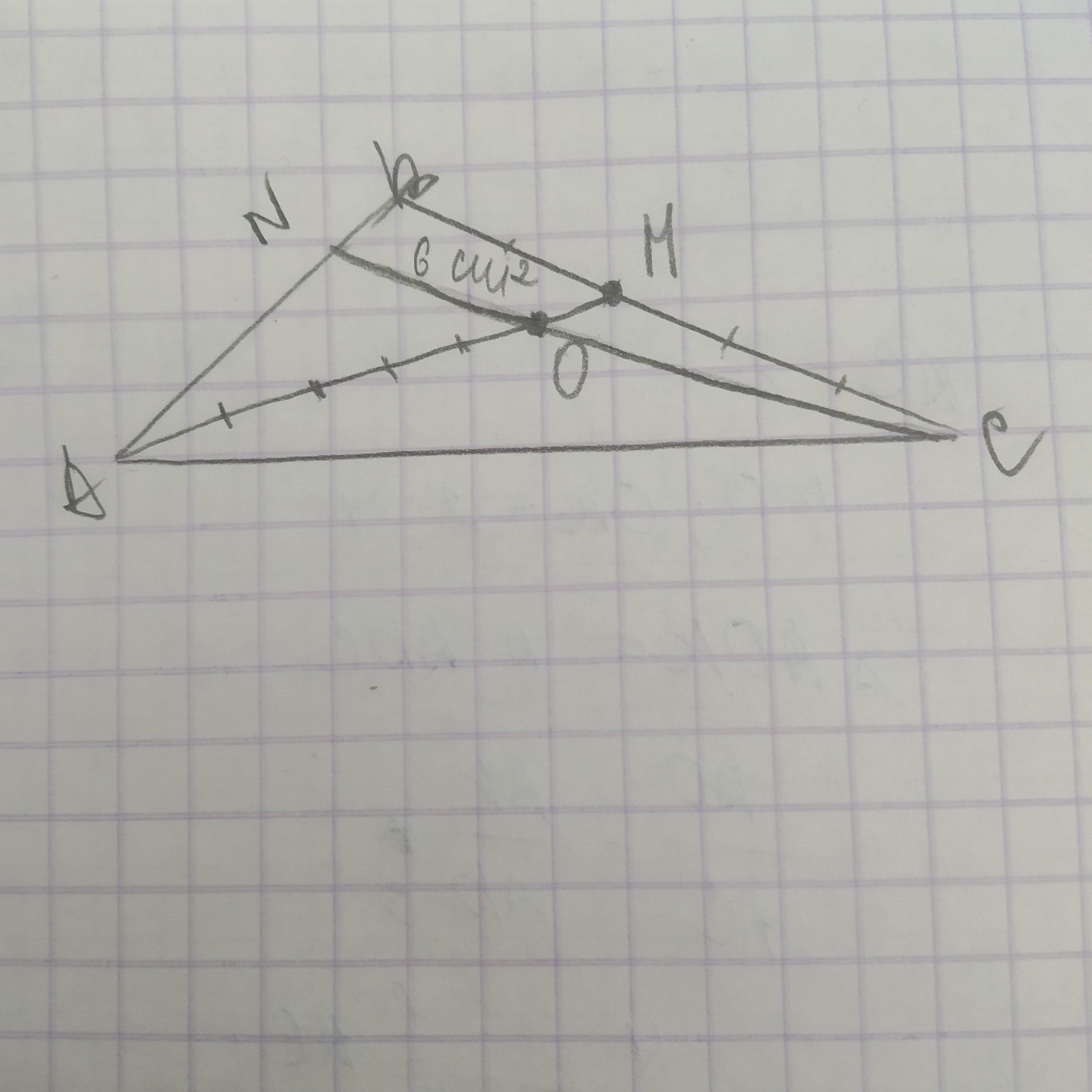
На сторонах AB и ВС треугольника АВС взяты точки М и N соответственно,СМ:МВ=3:2. Прямая СN пересекает АМ в точке О и делит её в отношении АО:ОМ=5:1. Найти площадь треугольника ABC если площадь четырехугольника NBMO равна 6см^2..

Приложения:

Ответы

Ответ дал: Аноним

За теоремою Менелая:

$dfrac{BN}{AN}cdot dfrac{AO}{OM}cdot dfrac{CM}{BC}=1\ \ dfrac{BN}{AN}cdot 5cdot dfrac{3}{5}=1\ \ dfrac{BN}{AN}=dfrac{1}{3}$

$dfrac{S_{ABM}}{S_{ABC}}=dfrac{BM}{BC}=dfrac{2}{5}\ \ dfrac{S_{AON}}{S_{ABM}}=dfrac{ANcdot AO}{ABcdot AM}=dfrac{3cdot 5}{4cdot 6}=dfrac{5}{8}$

$S_{BMON}=dfrac{3}{8}S_{ABM}=dfrac{3}{8}cdot dfrac{2}{5}S_{ABC}=dfrac{3}{20}S_{ABC}\ \ S_{ABC}=dfrac{20}{3}S_{BMON}=dfrac{20}{3}cdot 6=40$

Похожие вопросы

Английский язык

2 года назад

Українська мова

2 года назад

Математика

2 года назад

Физика

2 года назад

Математика

8 лет назад

Математика

8 лет назад

Химия

9 лет назад

Химия

9 лет назад