100 баллов.

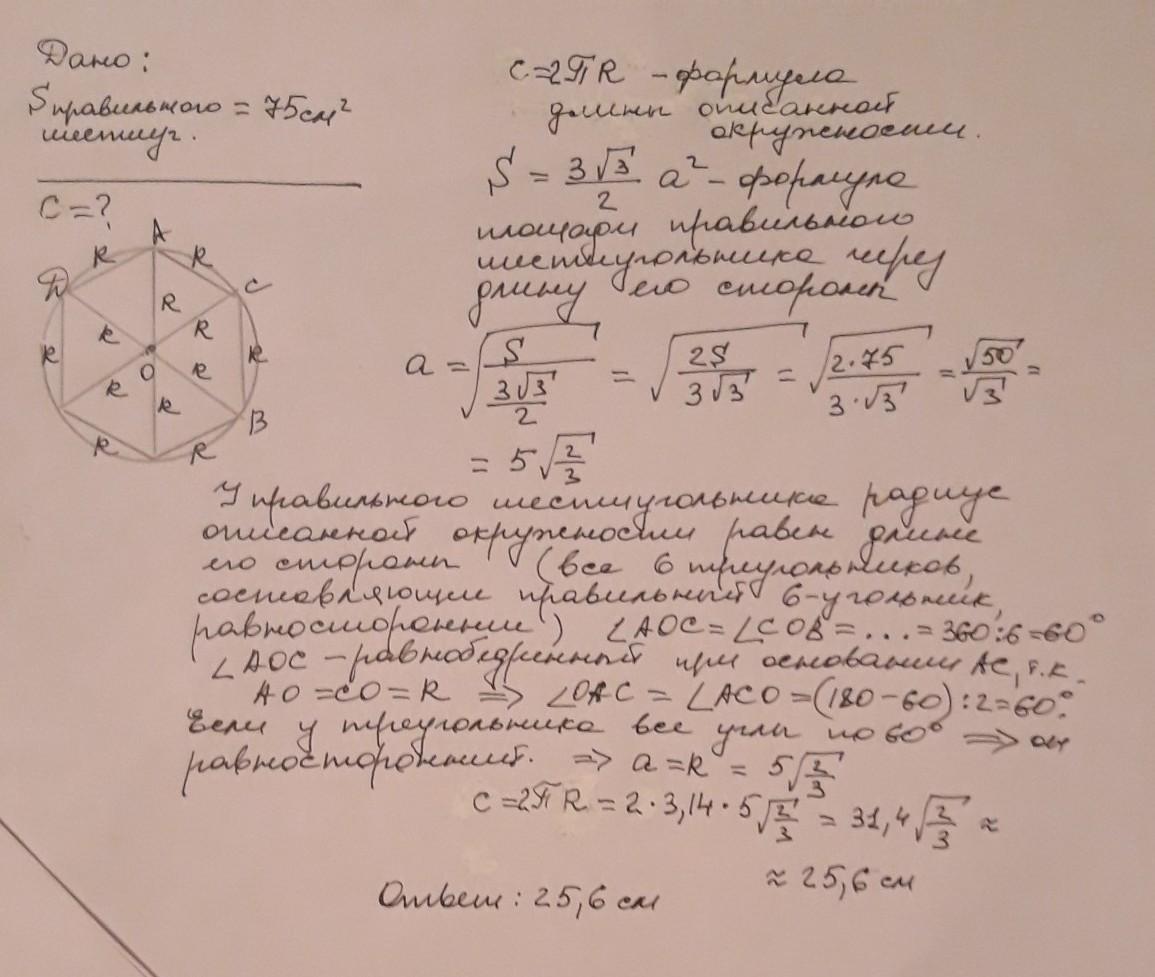
Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 75 см2

Ответ :

Найти длину описанной окружности.

Иными словами, надо найти длину окружности, описанной около  правильного шестиугольника. Ее радиус совпадает со стороной шестиугольника. Любой правильный шестиугольник можно разбить на шесть правильных треугольников. Площадь одного такого треугольника, как известно, равна а²√3/4, тогда площадь шестиугольника равна 6*а²√3/4=3√3а²/2, поэтому 75=3√3а²/2, откуда 75*2/(3√3)=а²=R²⇒R=√(50/√3)=5√2/(3¹/⁴), а длина окружности, равна 2πR=2π*5√2/(3¹/⁴)=10π(√(2/√3)) /см/

Это точное значение, если его округлить, π≈3.14, то получим примерный результат. 10*3.14*√1.1547005384≈33.74/см/