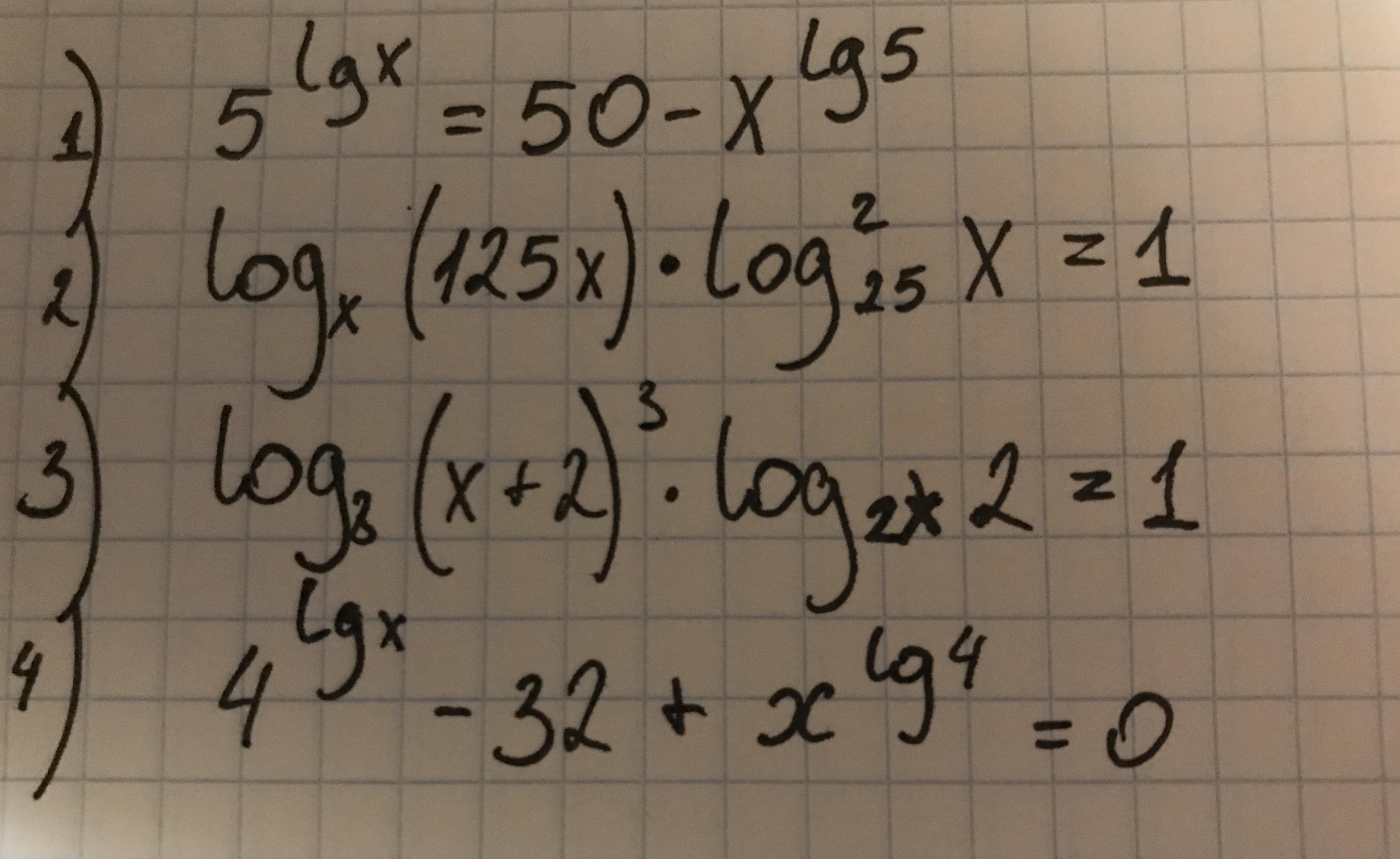Предмет: Алгебра
Автор: satanakorovka
Вопрос задан 7 лет назад

< >

Логарифмы~~~~

Поможете? Хоть намекнуть что-нибудь))

Приложения:

Ответы

Ответ дал: Medved23

0

1) Воспользуемся свойством $a^{log_bc}=c^{log_ba}$

$5^{lg x}=50-x^{lg5}; OD3: x>0, xneq 1.\\5^{lg x}=50-5^{lg x},\\2cdot5^{lg x}=50,\5^{lg x}=25;\\5^{lg x}=5^2Rightarrow lg x =2Rightarrow x =10^2, x=100.$

2) ОДЗ: $left { {{x>0} atop {xneq 1}} right.$

Распишем первый множитель как логарифм произведения: $log_x(125x)=log_x125+log_xx=1+3log_x5=1+frac{3}{log_5x}$

Распишем второй множитель:

$log_{25}^2x=(log_{5^2}x)^2=(frac{1}{2}log_5x)^2=frac{1}{4}log_5^2x$

Сделаем замену: $log_5x=t$

Имеем уравнение

$(1+frac{3}{t})frac{1}{4}t^2=1 \\frac{1}{4}t^2+frac{3t^2}{4t}-1=0;\\frac{1}{4}t^2+frac{3}{4}t -1=0|cdot4,\\t^2+3t-4=0 Rightarrow t_1=-4, t_2=1.\left [ {{log_5x=-4} atop {log_5x=1}} right. Rightarrow x_1=frac{1}{625}, x_2=5.$

$3) log_8(x+2)^3cdotlog_{2x}2=1;\OD3:left { {{x>0} atop {xneq 0,5}} right.\\frac{3}{3}log_2(x+2)cdotfrac{1}{log_2(2x)}=1;\frac{log_2(x+2)}{log_22+log_2x}=1,\\ log_2(x+2)-1=log_2x;\log_2(frac{x+2}{2})=log_2x\frac{x+2}{2}=x,\\2x=x+2Rightarrow x=2.$

$4) OD3: left { {{x>0} atop {xneq 1}} right. \\4^{lg x}+4^{lg x}=32,\\2cdot4^{lg x}=32,\\4^{lg x}=16,\\4^{lg x}=4^2Rightarrow lg x =2Rightarrow x = 10^2, x= 100.$

Похожие вопросы

Українська мова

1 год назад

У ліс завітала чарівниця зима .Дерева закутала в снігові шуби . На пеньки одягла білі шапки. Усе біле. Ось тільки лисиця залишилася рудою. Підкресли слово у якому звуків більше ніж був .Побудуй його

Английский язык

1 год назад

Помогмте пожалуйста. завтра сдавать

Геометрия

2 года назад

Периметр равнобедренного треугольника ACB с основанием AC равен 40 см, а периметр равностороннего треугольника ACD равен 18 см. Найди длину боковой стороны равнобедренного треугольника.

Математика

2 года назад

число увеличили на 36 и оно составило 7/36 от исходного числа.Найти исходное число.

Алгебра

8 лет назад

Представьте в виде произведения: 8n^4-n^7 Решить уравнение: (х^2-1)(х^2+3)=(х^2+1)^2+х. срочно прошу

Математика

8 лет назад

Пожалуйста помогите решить уравнение 873 - n:3=549

Математика

9 лет назад

помогите пожалуйста .... 1)Найди значение выражения 7+3×(8+12). 2) найди значение выражения 43-27 3) найди значение выражения 12012.3170.4. 4 ) масса шести одинаковых ящиков изюмом равна 180 кг масса

Физика

9 лет назад

Три тела подняты над поверхностью земли и расположены так, как это показано на рисунке. Максимальной потенциальной энергией обладает тело... 1) 1 2) 2 3) 3