ДАМ 35 БАЛЛОВ!!!
Найдите площадь боковой поверхности правильной четырехугольной усечённой пирамиды стороны оснований которой равны 6 и 22 см, а боковое ребро 4 корень из 5 см.

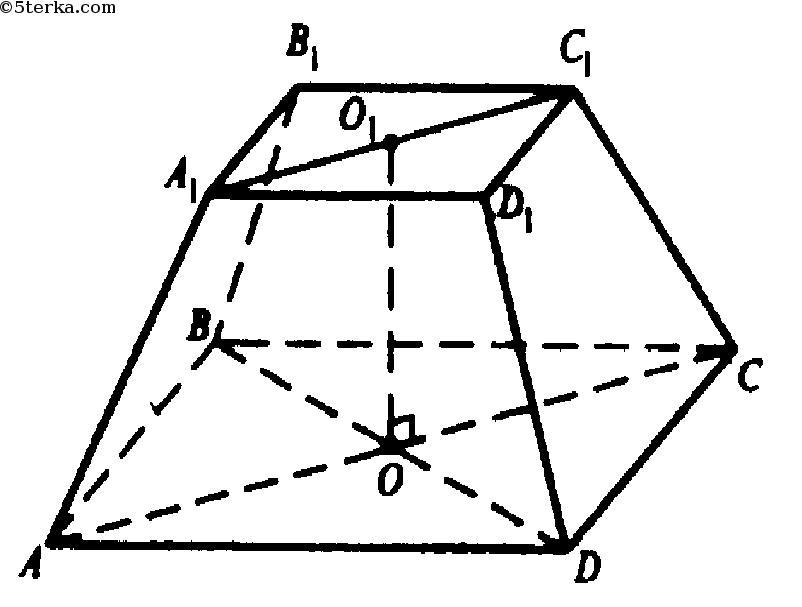
Пусть дана правильная четырехугольная усеченная пирамида , где и — квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды см.

Найдем площадь боковой поверхности заданной пирамиды.

Для того чтобы ее найти, следует найти площадь одной боковой грани (равнобедренной трапеции) и ее умножить на 4.

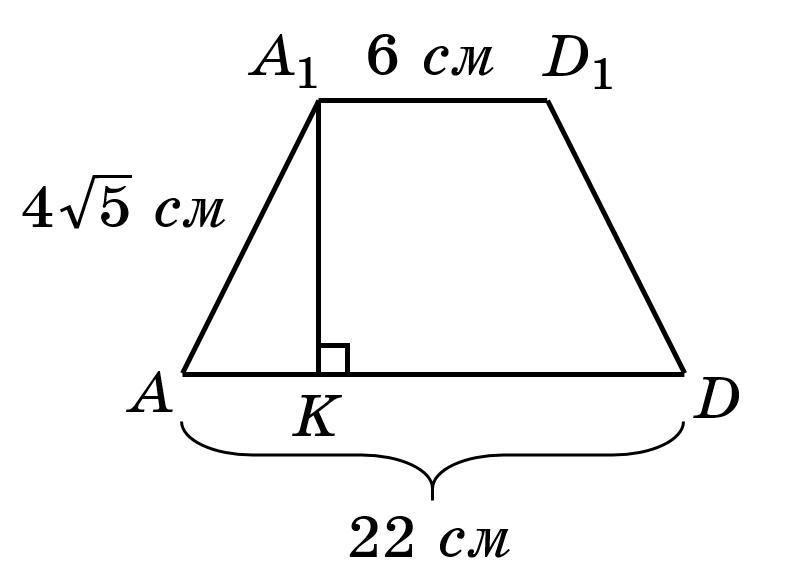
Рассмотрим равнобедренную трапецию

Проведем в трапеции высоту

Найдем см

Рассмотрим прямоугольный треугольник

По теореме Пифагора: см.

Следовательно, площадь трапеции равна

см².

Таким образом, см².

Ответ: 224 см².