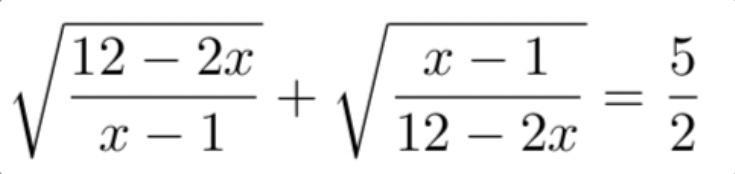Решите пожалуйста уравнение

Приложения:

Ответы

Ответ дал: Kat14z

Пусть 12-2х / х-1 =t

Тогда √t + √1/t = 5/2

t=1/4. t=4.

Вернемся к исходной переменной:

12-2х / х-1=1/4. 12-2х / х-1=4.

х=49/9. х=8/3.

Ответ: 49/9 ; 8/3.

Ответ дал: nafanya2014

Замена переменной:

$sqrt{frac{12-2x}{x-1} }=t; \ \ sqrt{frac{x-1}{12-2x}}=frac{1}{t} ; \\ t>0; tneq 0$

Решаем уравнение:

$t+frac{1}{t}=frac{5}{2}\ \ 2t^2-5t+2=0\ D=25-16=9\ \ t_{1}=frac{1}{2} ;t_{2}=2$

Обратная замена:

$sqrt{frac{12-2x}{x-1} }=frac{1}{2} \ \ frac{12-2x}{x-1} }=frac{1}{4} \ \ 4cdot(12-2x)=x-1\ \ 48-8x=x-1\ \ 49=9x\ x=frac{49}{9}$

$sqrt{frac{12-2x}{x-1} }=2 \ \ frac{12-2x}{x-1} }=4 \ \ 12-2x=4cdot(x-1)\ \ 12-2x=4x-4\ \ 16=6x\ \ x=frac{16}{6} \ \ x=frac{8}{3}$

О т в е т $frac{49}{9}; frac{8}{3}$

Похожие вопросы

Английский язык

2 года назад

Русский язык

2 года назад

Биология

2 года назад

Математика

2 года назад

Математика

8 лет назад

Математика

8 лет назад

История

9 лет назад

Литература

9 лет назад