помогите срочно даю 20 баллов​

Ответ:

Объяснение:

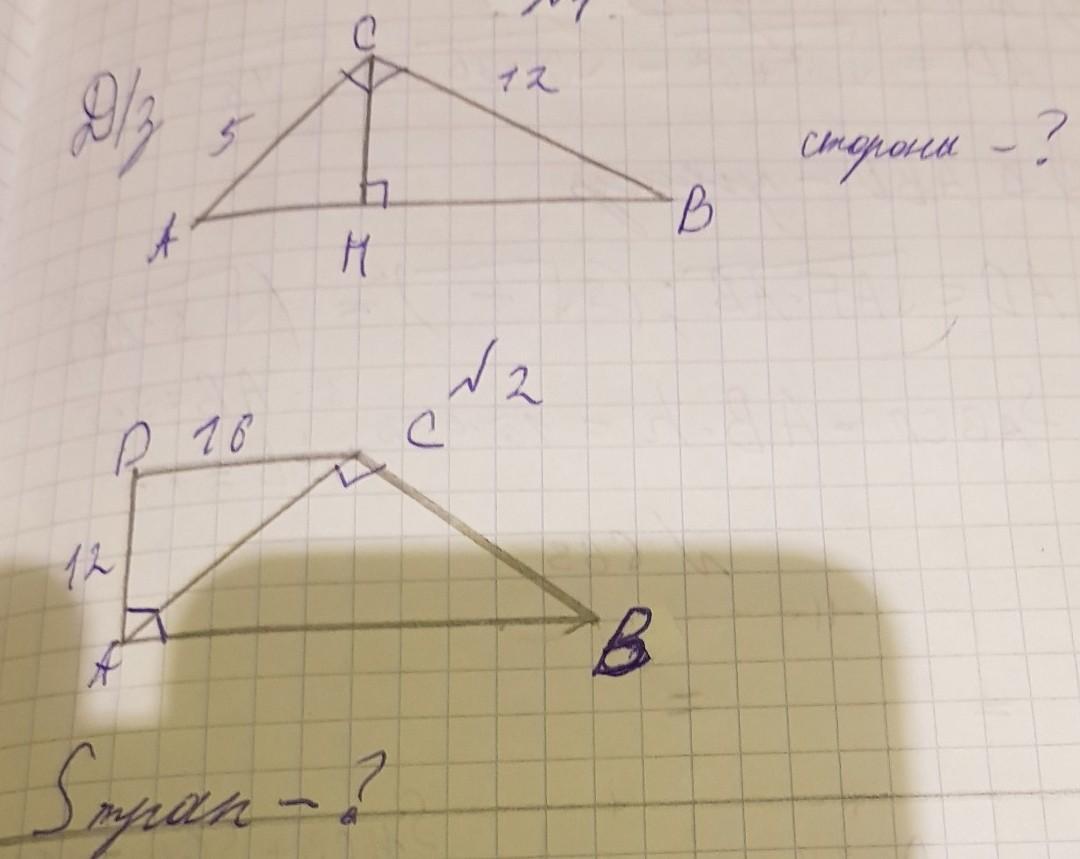
Рассмотрим ΔАВС-прямоугольный, по т. Пифагора АВ²=АС²+СВ².

АВ²= 25+144, то АВ²=169, АВ=13.

Если в прямоугольном треугольнике опущена высота на гипотенузу, то каждый из катетов есть среднее пропорциональное между всей гипотенузой и его проекцией на гипотенузу.

АС=√АН*АВ, 5=√АН*13, 25=АН*13, АН=25/13

ВС=√ВН*АВ, 12=√ВН*АВ, 144=ВН*13  ,ВН=144/13.

Если в прямоугольном треугольнике опущена высота на гипотенузу, то высота является средним пропорциональным между проекциями катетов на гипотенузу.

СН=√АН*ВН ,СН=√(25/13)*(144/13)=(5*12)/13=60/13