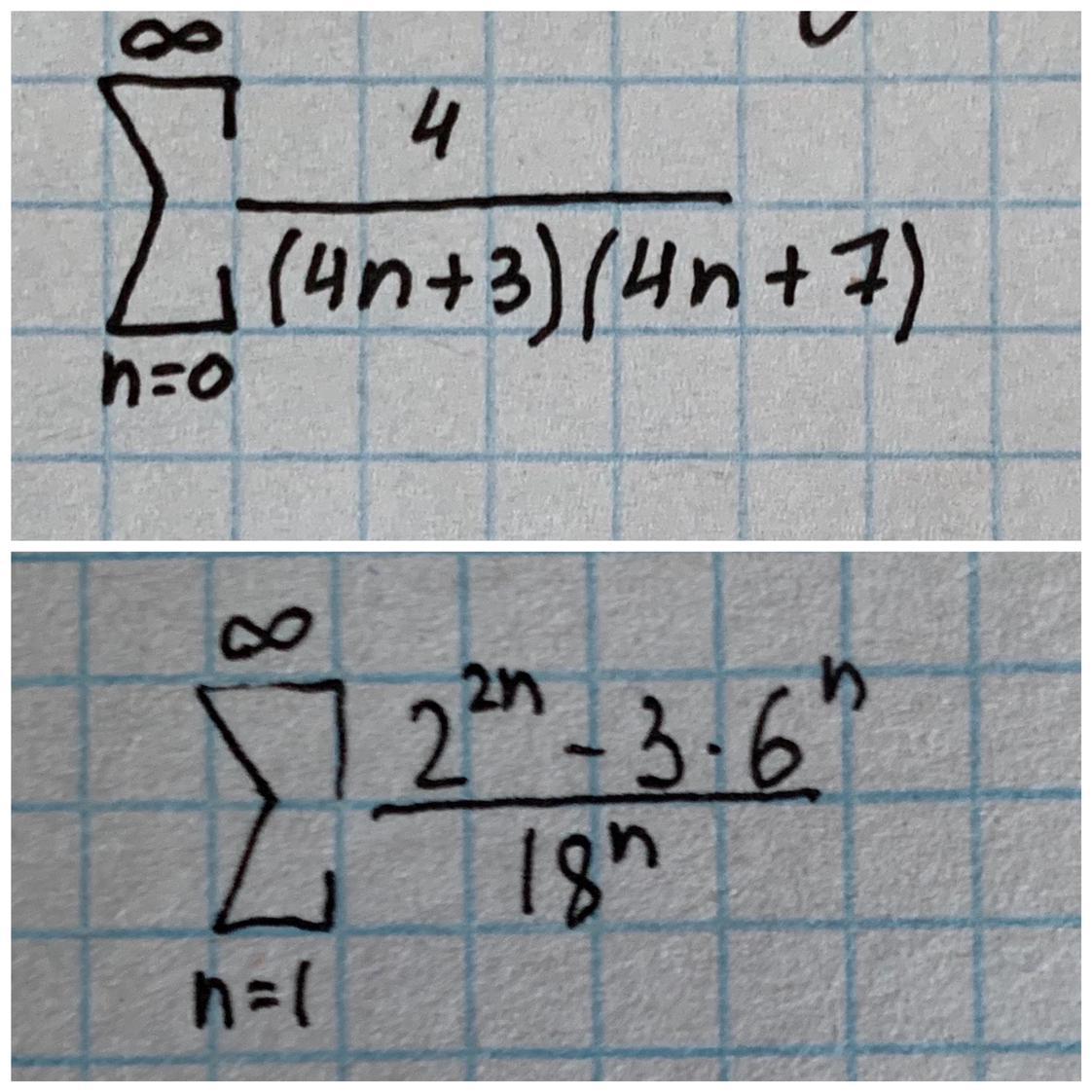Предмет: Алгебра
Автор: x0xx0x0x
Вопрос задан 7 лет назад

Помогите, пожалуйста
Нужно доказать сходимость ряда и найти его сумму

Приложения:

Ответы

Ответ дал: igorShap

Сумма ряда равна пределу его частных сумм. Если предел частных сумм существует и конечен, то ряд сходится.

$1)dfrac{4}{(4n+3)(4n+7)}=dfrac{1}{4n+3}-dfrac{1}{4n+7}\ sumlimits_{n=0}^k dfrac{4}{(4n+3)(4n+7)}=sumlimits_{n=0}^k dfrac{1}{4n+3}-dfrac{1}{4n+7}=dfrac{1}{3}-dfrac{1}{7}+dfrac{1}{7}-dfrac{1}{11}+...+dfrac{1}{4k+3}-dfrac{1}{4k+7}=dfrac{1}{3}-dfrac{1}{4k+7}\ =>sumlimits_{n=0}^infty dfrac{4}{(4n+3)(4n+7)}=limlimits_{ktoinfty}sumlimits_{n=0}^k dfrac{4}{(4n+3)(4n+7)}=limlimits_{ktoinfty}dfrac{1}{3}-dfrac{1}{4k+7}=dfrac{1}{3}$

$2)a_n=dfrac{2^{2n}-3*6^n}{18^n}=(dfrac{2}{9})^n-3*(dfrac{1}{3})^n\ sumlimits_{n=1}^k a_n=sumlimits_{n=1}^k (dfrac{2}{9})^n-3*sumlimits_{n=1}^k(dfrac{1}{3})^n=dfrac{frac{2}{9}((frac{2}{9})^k-1)}{frac{2}{9}-1}-3*dfrac{frac{1}{3}((frac{1}{3})^k-1)}{frac{1}{3}-1}=-dfrac{2}{7}((frac{2}{9})^k-1)+dfrac{3}{2}((frac{1}{3})^k-1)$

$sumlimits_{n=1}^infty a_n=limlimits_{ktoinfty}sumlimits_{n=1}^k a_n=limlimits_{ktoinfty}-dfrac{2}{7}((frac{2}{9})^k-1)+dfrac{3}{2}((frac{1}{3})^k-1)=dfrac{2}{7}-dfrac{3}{2}=-dfrac{17}{14}$