В треугольник вписана окружность. Вычисли углы треугольника, если ∢ OMN= 35° и ∢ LNO= 36°. 12ok.png ∢ M= °; ∢ N= °; ∢ L= °.
Приложения:
Ответы
Ответ дал:
0
Решение:
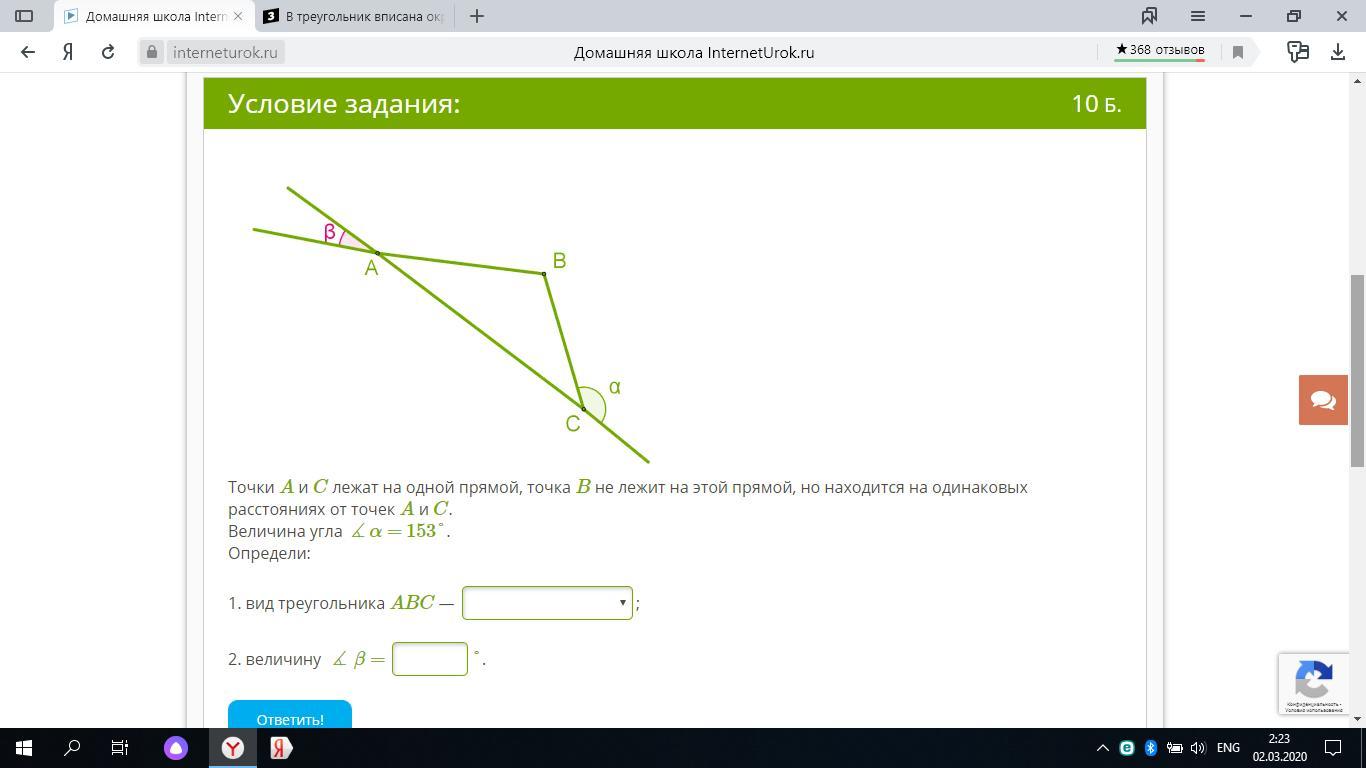
1. Так как ∠BCA и ∠α - смежные, то:
∠BCA = 180° - ∠α = 180° - 153° = 27°
2. Так как по условию точка B находится на одинаковых расстояниях от точек A и C, то отрезки AB и BC будут равны, следовательно этот треугольник ABC - равнобедренный с основанием AC.
3. Так как треугольник ABC - равнобедренный, то:
∠BAC = ∠BCA = 27° (по свойству равнобедренного треугольника)
4. Так как ∠β и ∠BAC - вертикальные, а вертикальные углы равны, то:
∠β = ∠BAC = 27°
Ответ:
1. вид треугольника ABC - равнобедренный
2. величину ∠β = 27°
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад