100 баллов, ПРЕДЕЛЫ!!!
Решите пределы, не применяя производную!
ответы:
112: -1
107: 14
98: -2
106:-1/24
113: корень из 3
115: - корня из 2
131: 1

Приложения:

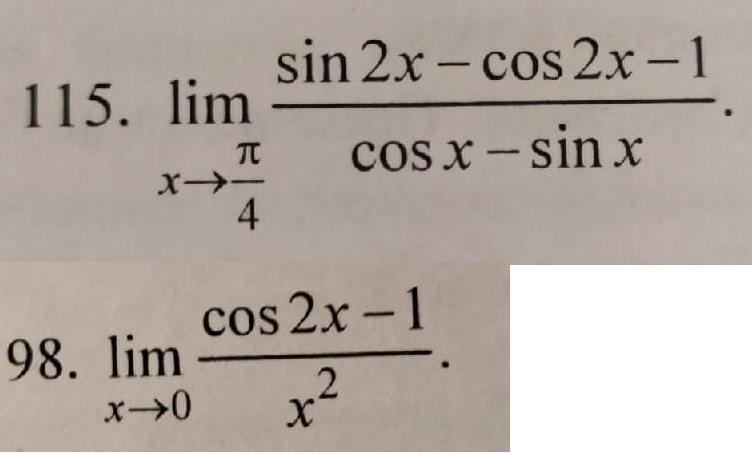
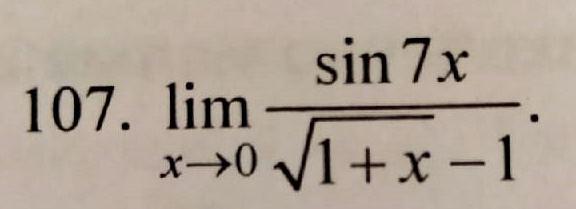
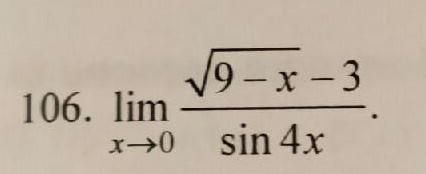
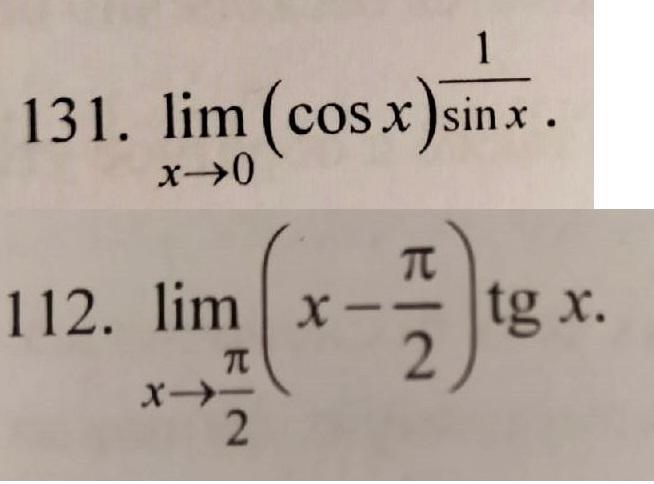
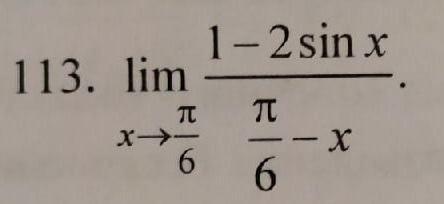
Ответы

Ответ дал: NNNLLL54

$115.; ; ; limlimits _{x to pi /4}frac{sin2x-cos2x-1}{cosx-sinx}=limlimits _{x to pi /4}frac{2, sinx, cosx-(cos^2x-sin^2x)-(sin^2x+cos^2x)}{cosx-sinx}=\\=limlimits _{x to pi /4}frac{2, cosx, (sinx-cosx)}{-(sinx-cosx)}=limlimits _{x to pi /4}, (-2cosx)=-2cdot cosfrac{pi}{4}=-2cdot frac{sqrt2}{2}=-sqrt2$

$98.; ; ; limlimits _{x to 0}frac{cos2x-1}{x^2}=Big[; 1-cosalpha =2sin^2frac{alpha }{2}; Big]=limlimits _{x to 0}frac{-2sin^2x}{x^2}=\\=Big[; sinxsim x; ,; esli; xto 0; ;; ; sin^2x=(sinx)^2sim x^2; Big]=limlimits _{x to 0}frac{-2cdot x^2}{x^2}=-2$

$107.; ; limlimits _{x to 0}frac{sin7x}{sqrt{1+x}-1}=limlimits _{x to 0}frac{7x, cdot , (sqrt{1+x}+1)}{(sqrt{1+x}-1)(sqrt{1+x}+1)}=limlimits _{x to 0}frac{7x, cdot , (sqrt{1+x}+1)}{(1+x)-1}=\\=limlimits_{x to 0}frac{7x, cdot , (sqrt{1+x}+1)}{x}=limlimits _{x to 0}, 7(sqrt{1+x}+1)=7cdot (sqrt1+1)=7cdot 2=14$

$106.; ; limlimits _{x to 0}frac{sqrt{9-x}-3}{sin4x}=limlimits _{x to 0}frac{(sqrt{9-x}-3)(sqrt{9-x}+3)}{4x, cdot , (sqrt{9-x}+3)}=limlimits _{x to 0}, frac{(9-x)-9}{4x(sqrt{9x-3}+3)}=\\=limlimits _{x to 0}, frac{-1}{4, (sqrt{9-x}+3)}=-frac{1}{4cdot 6}=-frac{1}{24}$

$131.; ; ; limlimits _{x to 0}, (cosx)^{frac{1}{sinx}}=limlimits _{x to 0}, Big(1+(cosx-1)Big)^{frac{1}{cosx-1}cdot frac{cosx-1}{sinx}}=\\=limlimits _{x to 0}Big(Big(1+(cosx-1)Big)^{frac{1}{cosx-1}}Big)^{frac{cosx-1}{sinx}}=e^{limlimits_{x to 0}frac{-(1-cosx)}{sinx}}=e^{limlimits_{x to 0}frac{-2sin^2x/2}{x}}=\\=e^{limlimits_{x to 0}frac{-2cdot frac{x^2}{4}}{x}}=e^{limlimits_{x to 0}frac{-x}{2}}=e^0=1$

$112.; ; limlimits _{x to pi /2}Big(x-frac{pi}{2}Big)cdodt tgx=Big[; t=x-frac{pi}{2}; ,; tto 0; Big]=limlimits _{t to 0}; (, tcdot tg(t+frac{pi}{2}), )=\\=limlimits _{t to 0}; frac{tcdot sin(t+frac{pi}{2})}{cos(t+frac{pi}{2})}=limlimits _{t to 0}; frac{tcdot sin(t+frac{pi}{2})}{-sint}=limlimits _{t to 0}; frac{tcdot sin(t+frac{pi}{2})}{-t}=limlimits _{t to 0}; (-sinfrac{pi}{2})=-1$

$113.; ; limlimits _{x to pi /6}frac{1-2sinx}{frac{pi}{6}-x}=limlimits _{x to pi /6}frac{2, (frac{1}{2}-sinx)}{frac{pi }{6} -x}=2limlimits _{x to po /6}frac{sinfrac{pi}{6}-sinx}{frac{pi}{6}-x}=\\=2limlimits _{x to pi /6}frac{2, sin(frac{pi}{12}-frac{x}{2})cdot cos(frac{pi}{12}+frac{x}{2})}{frac{pi}{6}-x}=Big[; sinasim a,; ato 0; Big]=4limlimits _{x to pi /6}frac{(frac{pi}{12}-frac{x}{2})cdot cos(frac{pi}{12}+frac{x}{2})}{frac{pi -6x}{6}}=$

$=4limlimits _{x to pi /6}frac{frac{pi -6x}{12}cdot cosfrac{pi}{6}}{frac{pi -6x}{6}}=4limlimits_{x to \pi /6}, frac{(pi -6x)cdot frac{sqrt3}{2}}{12cdot frac{pi -6x}{6}}=4limlimits _{x to pi /6}frac{sqrt3}{4}=sqrt3$