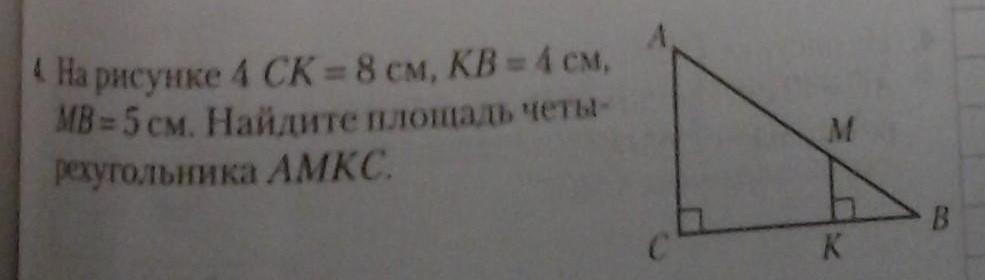Помогите решить N°4. ​

Ответ:

Площадь AMKC = 48 ().

Объяснение:

Искомый четырехугольник AMKC - прямоугольная трапеция с основаниями АС и МК и высотой СК, т.к. (АС || МК)⊥СВ.

Площадь трапеции: . h=CK=8 (см). Нужно найти основания a (АС) и b (МК).

По теореме о пропорциональных отрезках находим длину АМ:

⇒ .

Находим недостающие стороны по т. Пифагора у двух прямоугольных треугольниках ABC и МВК:

Находим площадь четырехугольника/трапеции:

Ответ:

решение

Объяснение:

(MK*KB)/2 = 6см^2

CB = CK+KB = 8+4 = 12см

AC = MK*3 = 9см

S ABC = (AC*CB)/2 = (9*12)/2 = 54см^2

54-6 = 48см^2

Ответ: S(AMKC) = 48см^2