Ребята помагите очень срочно ​

Ответ: 70.................................

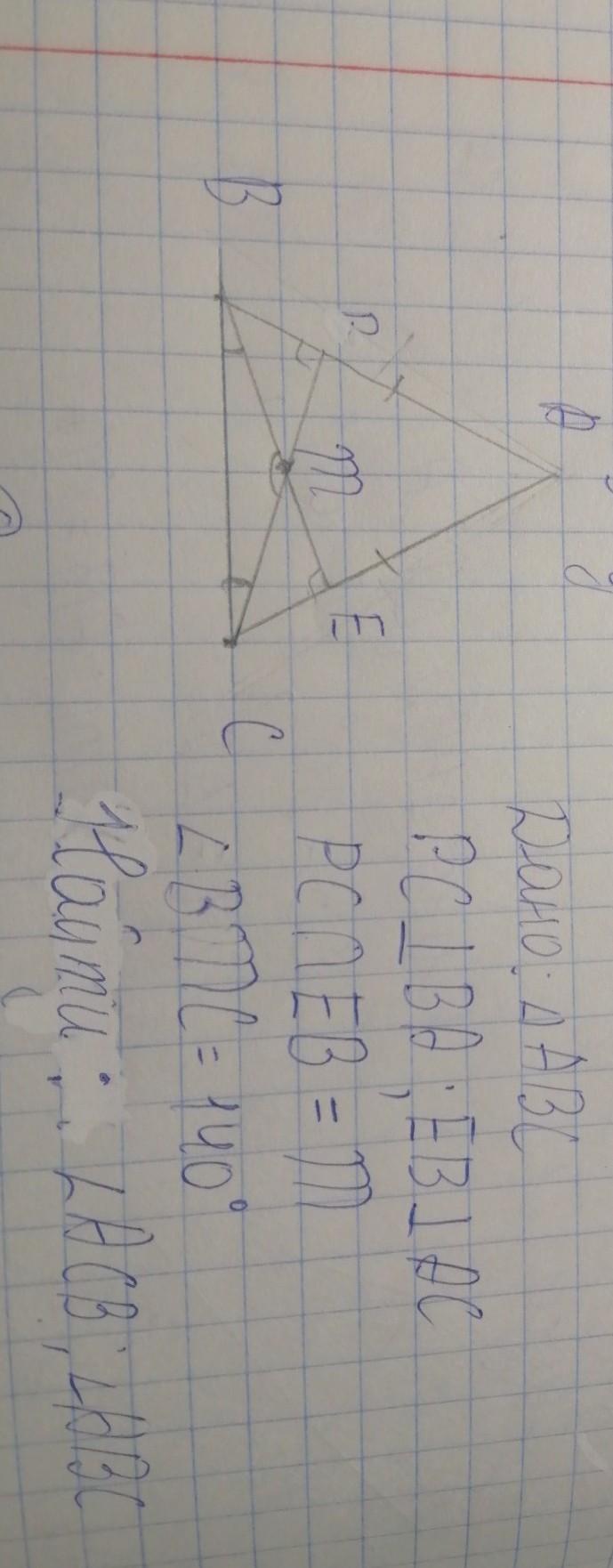
Дано :   Δ ABC        AB = AC  или  AE  = AP  (усл.  эквивалентны)

BE ⊥ AC , CP ⊥ AB ,  CP ∩ BE = M ,∡BMC =140°

--------------------------

∡ABC _ ?  ∡ACB_?

Ответ:  ∡ABC =∡ACB =70°

Объяснение:  

если  AE  = AP  ⇒  Δ AEB = Δ APC  (по катету и острому углу A) ⇒

AB = AC  ,т.е.  треугольник  ABC_ равнобедренный

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

Для  четырехугольника   APME :

∡A +∡PME+90°+90° =360° ⇒  ∡A+ ∡PME=180° ⇔

∡A= 180° - ∡PME = 180°- ∡BMC =180°- 140° =40°

ΔBAC _равнобедренный

∡ABC =∡ACB =(180° -∡A)/2 =(180° -40°)/2  = 70° .

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

можно и так

               Δ BCP                   Δ СBE

∡BCP = 90° - ∡ABC     =  90° - ∡ACB  = ∡CBE  ,

т.е. треугольник  BMC_ равнобедренный ,следовательно

∡BCP = ∡CBE = (180° - ∡BMC ) /2 = (180° - 140° ) /2 =20°

∡BCP =90° - ∡ABC ⇒  ∡ABC = 90° - ∡BCP = 90° -20° =70°