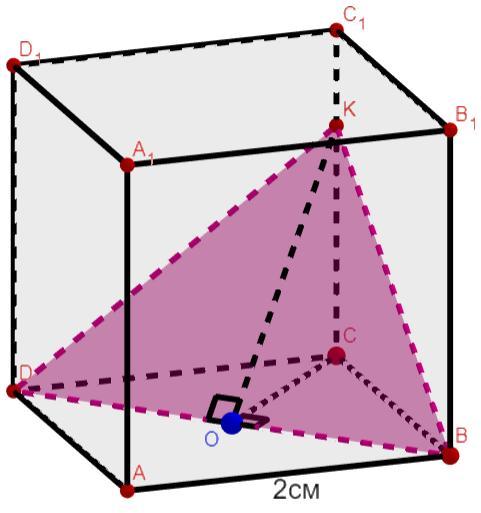
Ребро куба abcda1b1c1d1 равно 2см . Через диагональ основания bd под углом45° к плоскости основания проведена плоскость bdk , пересекающая боковое ребро в точке k . Найдите площадь треугольника bdk

Не ограничивая общности K∈CC₁

Пусть O - середина BD.

ΔDCB - равнобедренный (C-вершина).

ΔBCK=ΔDCK по двум катетам (BC=DC как рёбра, CK - общий катет), поэтому BK=DK.

ΔDKB - равнобедренный (K-вершина).

Медиана проведённая из вершины равнобедренного треугольника является высотой. Поэтому KO⊥BD и CO⊥BD. Из чего следует, что ∠COK - линейный угол, двугранного угла CBDK, который по условию равен 45°.

ΔOCK - прямоугольный (∠С=90°), с острым углом в 45°, поэтому OK=OC:cos45°.

Диагональ (BD) квадрата ABCD, равна √2·BC=2√2см

OC - половина диагонали квадрата.

Откуда OC= см

OK= см

S(BKD) = OK·BD/2 = см².

Ответ: 2√2 см².