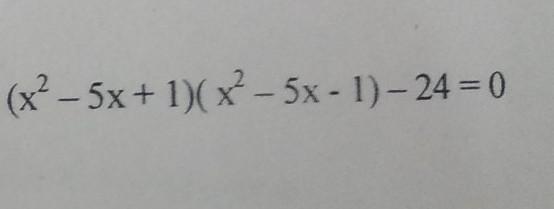решить уравнение способом введения новой переменной​

Заменим х²-5х = t. Тогда наше уравнение примет вид:

Обратная замена:

1)

2)

Решаем методом замены х^2-5х=у

тогда у нас уравнение примет вид (у+2)(у-1)=28

у1+у2=1; у1•у2+у-30=0

у1=6; у2=5; х^2-5х= -6

х^2-5х+6=0; х1=5; х2=1

х^2-5х=5; х^2-5х-5=0

Д=5^2-4•1•(-5)=25+20=45=3V5

x1=(5+3V5):2; x2=(5-3V5):2

Ответ: х1=5, х2=1, х3=(5+3V5):2, x4=(5-3V5):2