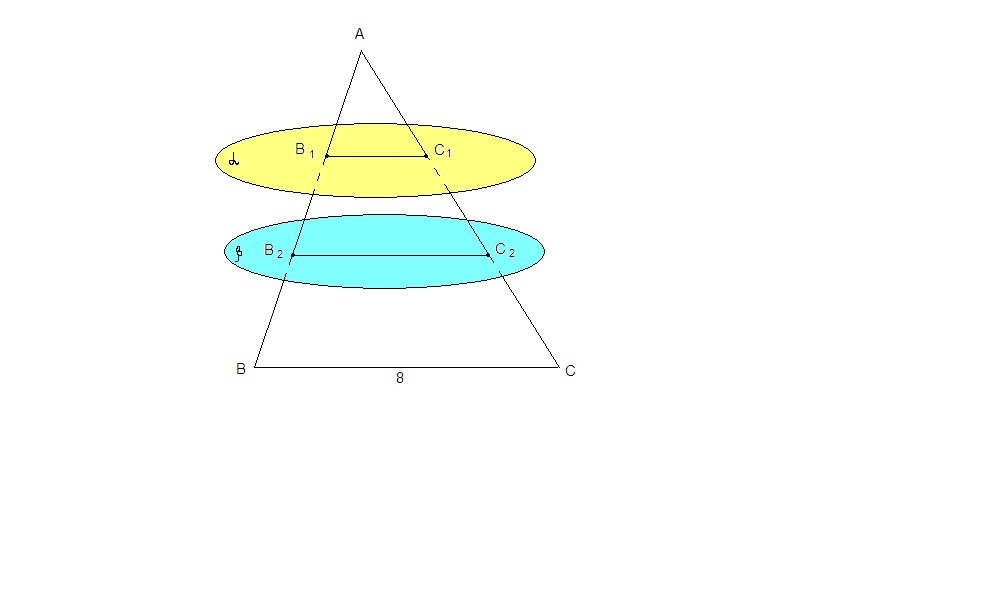
помогите.пожалуйста! Через точки B1 и B2 стороны AB равностороннего треугольника ABC проведены плоскости альфа и бета, параллельные прямой BC. 1) На какие фигуры делится этот треугольник плоскостями? 2) Вычислите периметры этих фигур, если AC=8 см и AB1=B1B2=B2B
Ответы
Ответ дал:
0
Плоскость треугольника АВС пересекает параллельные плоскости α и β по параллельным прямым.
ВС║В₁С₁║В₂С₂
По условию AB₁ = B₁B₂ = B₂B = 8/3 см, тогда по теореме Фалеса
AС₁ = С₁С₂ = С₂С = 8/3 см
ΔАВС подобен ΔАВ₁С₁ по двум углам (∠АВ₁С₁ = ∠АВС и ∠АС₁В₁ = ∠АСВ как накрест лежащие)
В₁С₁ : ВС = АВ₁ : АВ = 1 : 3
В₁С₁ = 8/3 см
ΔАВС подобен ΔАВ₂С₂ по двум углам (∠АВ₂С₂ = ∠АВС и ∠АС₂В₂ = ∠АСВ как накрест лежащие)
В₂С₂ : ВС = АВ₂ : АВ = 2 : 3
В₂С₂ = 2·8/3 = 16/3 см
а) треугольник АВС разбивается на
равносторонний треугольник АВ₁С₁;
трапецию В₂В₁С₁С₂;
трапецию ВВ₂С₂С.
б) Pab₁c₁ = (8/3) · 3 = 8 cм
Pb₂b₁c₁c₂ = 8/3 + 8/3 + 8/3 + 16/3 = 40/3 = 13 и 1/3 см
Pbb₂c₂c = 8/3 + 16/3 + 8/3 + 8 = 56/3 = 18 и 2/3 см
ВС║В₁С₁║В₂С₂
По условию AB₁ = B₁B₂ = B₂B = 8/3 см, тогда по теореме Фалеса
AС₁ = С₁С₂ = С₂С = 8/3 см
ΔАВС подобен ΔАВ₁С₁ по двум углам (∠АВ₁С₁ = ∠АВС и ∠АС₁В₁ = ∠АСВ как накрест лежащие)
В₁С₁ : ВС = АВ₁ : АВ = 1 : 3
В₁С₁ = 8/3 см
ΔАВС подобен ΔАВ₂С₂ по двум углам (∠АВ₂С₂ = ∠АВС и ∠АС₂В₂ = ∠АСВ как накрест лежащие)
В₂С₂ : ВС = АВ₂ : АВ = 2 : 3
В₂С₂ = 2·8/3 = 16/3 см
а) треугольник АВС разбивается на
равносторонний треугольник АВ₁С₁;
трапецию В₂В₁С₁С₂;
трапецию ВВ₂С₂С.
б) Pab₁c₁ = (8/3) · 3 = 8 cм
Pb₂b₁c₁c₂ = 8/3 + 8/3 + 8/3 + 16/3 = 40/3 = 13 и 1/3 см
Pbb₂c₂c = 8/3 + 16/3 + 8/3 + 8 = 56/3 = 18 и 2/3 см
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад