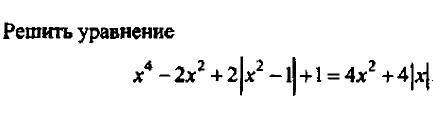Предмет: Алгебра
Автор: ВладимирБ
Вопрос задан 7 лет назад

< >

Решить уравнение
....................................

Приложения:

Ответы

Ответ дал: Evgenia4836

0

Решение во вложении:

Приложения:

Ответ дал: triggerbott

0

$x^4-2x^2+2|x^2-1|+1=4x^2+4|x|\ \ x^4-2x^2+1+2|x^2-1|+1=4x^2+4|x|+1\ \ Big(|x^2-1|+1Big)^2=Big(2|x|+1Big)^2\ \ Big(|x^2-1|+1Big)^2-Big(2|x|+1Big)^2=0\ \ Big(|x^2-1|+1-2|x|-1Big)Big(|x^2-1|+1+2|x|+1Big)=0\ \ Big(|x^2-1|-2|x|Big)Big(|x^2-1|+2|x|+2Big)=0$

Произведение равно нулю в том случае, когда хотя бы один из множителей равно нулю

$|x^2-1|-2|x|=0\ \ |x^2-1|=2|x|~~~Rightarrow~~~ Big(x^2-1Big)^2=4x^2~~Rightarrow~~ Big(x^2-1Big)^2-4x^2=0\ \ Big(x^2-2x-1Big)Big(x^2+2x-1Big)=0$ $x^2-2x-1=0\ D=4+4=8;~~sqrt{D}=2sqrt{2}\ x_{1,2}=dfrac{2pm2sqrt{2}}{2}=boxed{1pmsqrt{2}}$ $x^2+2x-1=0\ D=4+4=8;~~sqrt{D}=2sqrt{2}\ x_{1,2}=dfrac{-2pm2sqrt{2}}{2}=boxed{-1pmsqrt{2}}$

$|x^2-1|+2|x|+2=0$

Это уравнение решений не имеет, поскольку его левая часть положительная.

Ответ: $1pmsqrt{2};~ -1pmsqrt{2}$ .

Приложения:

Похожие вопросы

Русский язык

2 года назад

Что такое морфологический разбор?

Русский язык

2 года назад

Пожалуйста помогите( это 1 класс( как выполнить?(

Қазақ тiлi

2 года назад

1. Мәтінді оқыңдар. Перифразаларды пайдаланып, мәтін бойынша 5 сұрақ құраңдар.

Другие предметы

2 года назад

що таке холістичний підхід?

Математика

8 лет назад

решите все задания ......

История

8 лет назад

Результат политического развития стран Запада к концу 19 века: 1)Складывание либеральной демократии 2)Возникновение диктаторских режимов 3)Приход социалистических партий к власти 4)Отсутствие

Алгебра

9 лет назад

5(x+4)-3=3-2x Помогите

Математика

9 лет назад

Один делим на корень из 8 равно один делим на 16 в степен. -х