Длина окружности основания конуса равна 10пи см. Высота конуса равна 6см. Найти образующую конуса

l = 2 * pi* r

10 pi = 2 pi * r

r=10:2

r=5 cm

H = 6 cm

L² = r²+H²= 5²+6²= 25+36= 61

L = √61 

Ответ:

√61 см.

Объяснение:

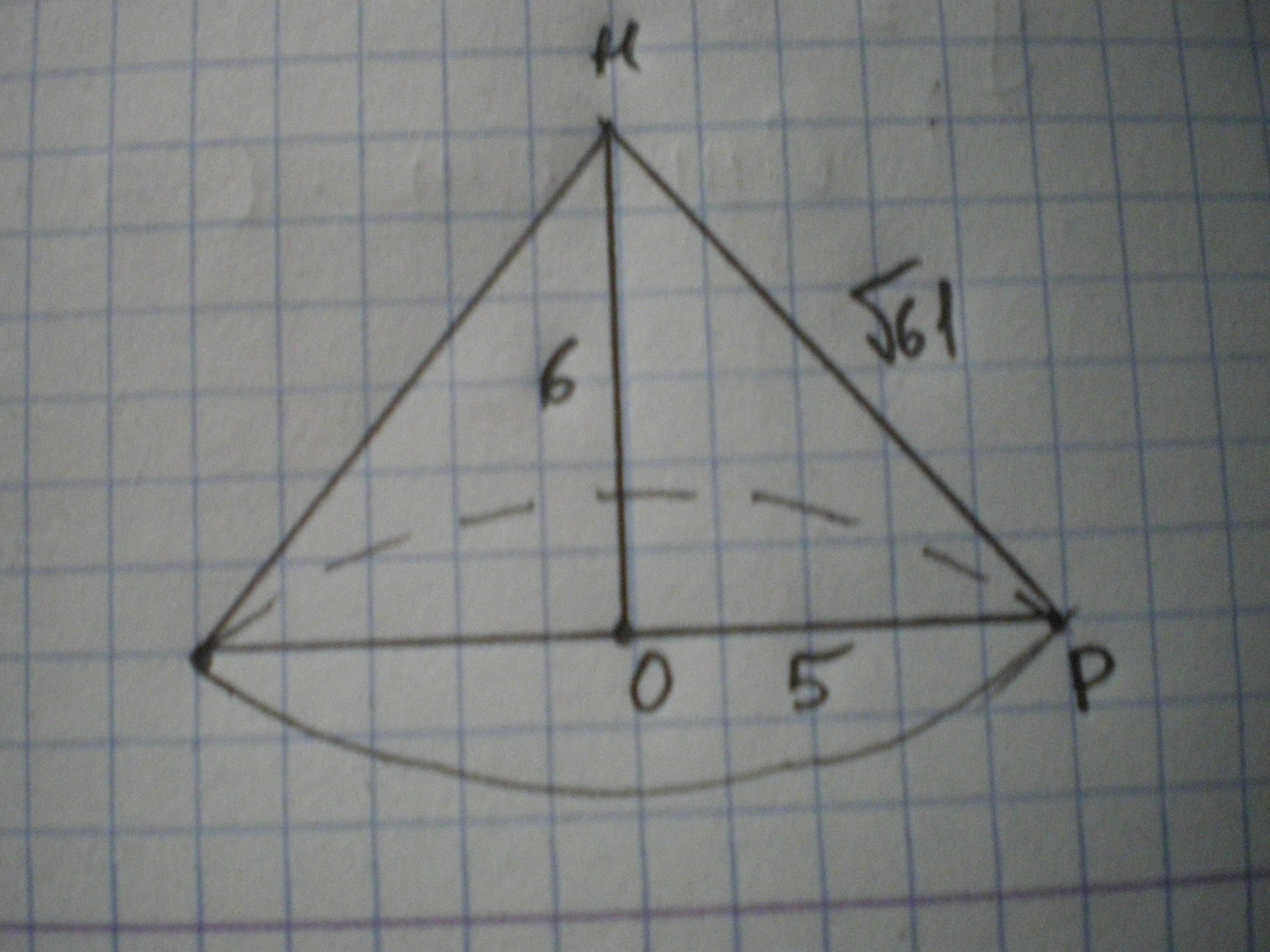
Дано: конус; длина окружности с центром в т. О=10π см; ОН - высота конуса;  ОН=6 см. Найти РН.

Найдем ОР - радиус окружности основания конуса, при том что длина окружности равна 2πr:

ОР=10π/2π=5 см.

Рассмотрим ΔОРН - прямоугольный, ОН=6 см, ОР=5 см:

по теореме Пифагора РН=√(ОН²+ОР²)=√(36+25)=√61 см.