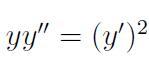Предмет: Алгебра
Автор: karakatiz
Вопрос задан 7 лет назад

Решить дифференциальное уравнение:

Приложения:

Ответы

Ответ дал: triggerbott

Тип: дифференциальное уравнение второго порядка, допускающее понижения порядка.

Пусть $u(y)=y'$ , тогда $y''=uu'$ , получаем

$uu'y=u^2\ \ u=0;~~~ u'y=u\ \ dfrac{du}{dy}cdot y=u~~~Rightarrow~~~ displaystyle int dfrac{du}{u}=int dfrac{dy}{y}~~~Rightarrow~~ ln|u|=ln|y|+ln C\ \ u=C_1y$

Выполним обратную замену

$y'=C_1y\ \ displaystyle int dfrac{dy}{y}=C_1int dx\ \ ln |y|=C_1x+C_2\ \ y=e^{C_1x+C_2}=C_1C_2e^x$

Если u = 0, то $y=c_1$

Ответ: $y=c_1$ или $y=C_1C_2e^x$

Ответ дал: karakatiz

Хорошо. Буду благодарен.

Похожие вопросы

Русский язык

2 года назад

Помогите написать сочинение на тему ЗОЖ здоровый образ жизни. НЕ С ИНТЕРНЕТА!!!

Українська мова

2 года назад

20 слів з правилом дeв’ятки даю 24 бала

Русский язык

2 года назад

Укажите строку, где все слова являются синонимами. Укажите правильный вариант ответа: Идти, шагать, бежать Бросать, кидать, швырять Алфавит, азбука, букварь Ураган, дождь, пурга

География

2 года назад

Это государство омывается вторым по площади океаном планеты и занимает седьмое место по площади территории на втором по размерам континенте Земли. Страна граничит с четырьмя государствами, два из

Математика

8 лет назад

Выполните действия в столбик: 42,165-22,165÷(0,61+3,42) В столбик пожалуйста очень надо и побыстрей!

Химия

8 лет назад

Главной составной частью мрамора является соль карбонат кальция. Напиши химическую формулу этой соли. Вычисли количество вещества каждого химического элемента в одном моле этого вещества. Результаты

История

9 лет назад

Кто был первым президентом России?

Математика

9 лет назад

Вычисли и сравни значения выражения.Запиши результаты сравнения с помощью знаков < > или =... 14+78*90-30 73+22*78-35 53-(12+39)*14+22-18 45+(7 •2)*(92 •1)-91