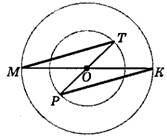
4. Отрезки МК и РТ являются диаметрами двух окружностей с общим центром О. Докажите, что прямые МТ и РК параллельны.(с рисунком)
5. Треугольник ABC — равнобедренный с основанием АС. На его биссектрисе BD взята точка М, а на основании — точка К, причем, МК || АВ. Найдите углы треугольника MKD, если ABC = 126°, BAC = 27°(без рисунка)
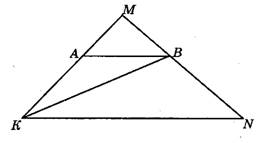
6. Докажите, что на рисунке прямые АВ и KN параллельны, если треугольник АВК — равнобедренный с основанием ВК, а луч KB является биссектрисой угла AKN.(с рисунком)
только решать нужно в формате дано доказать доказательство.
Ответы
Дано: МК и РТ - диаметры окружностей W1 и W2 соответственно. О-центр W1 и W2 .
Доказать, что МТ II РК.
Доказательство:
Рассмотрим треугольники МОТ и КОР. У них углы МОТ=КОР как вертикальные, ОТ=ОР как радиусы W1 , ОМ=ОК как радиусы W2 . Значит треуг. МОТ=КОР по первому признаку. Так как эти треуг-ки равны, то равны их соответствующие углы: угол ТМО=РКО, а ати углы являются накрест лежащими при прямых МТ и РК и секущейТР. Если накрест лежащие углы равны, то прямые параллельны. МТ II РК. Доказано.
Дано: треуг. АВС, АВ=ВС, BD-биссектриса, М принадлежит BD, К принадлежит АС, МК ІІ АВ, Угол АВС=126, ВАС=27. Найти углы треуг. МКD.
Решение:
Так как BD биссектриса, то угол АВD=126/2=63. Так как МК II AD, то углы АВD=KMD=63 как односторонние при параллельных АВ и КМ и секущей BD.
Угол АВС=MKD=27 как односторонние при папаллельных АВ и КМ и секущей АС.
В равнобедренном треуг. АВС BD является биссектрисой и высотой, значит угол ADB=KDM=90.
Ответ: 63, 27, 90.
Дано: треуг. MKN, А принадлежит МК, В принадлежит MN. Треуг АВК равнобедренный, АК=АВ. КВ-биссектриса АКN. Доказать, что АВ II KN.
Доказательство:
Так как КВ-биссектриса MKN, то угол МКВ=BKN, и так как треуг. КАВ равнобедренный с основанием КВ, то углы при основании равны АКВ=АВК. Отсюда следует, что АВК=BKN, а эти углы являются накрест лежащими при прямых АВ и KN и секущей ВК. Если накрест лежащие углы равны, то прямые АВ и КN параллельны. Доказано.
ЗАДАЧА 4. Рассмотрим треуг-ки МОТ и КОР: РО=ОТ (как радиусы), МО=ОК (как радиусы), углы МОТ и КОР равны как вертикальные. Значит, тр-ки равны по двум сторонам и углу между ними. Из равенства тр-ков следует равенство соответствующих углов: МТО=КРО и ТМО=РКО, а это внутренние накрест лежащие углы при прямых МТ и РК и секущих РТ и МК соответственно. Значит, прямые МТ и КР параллельны, ч.т.д.
ЗАДАЧА 5,6. Решение в прикрепленном файле
