Предмет: Математика
Автор: 1Kotek1
Вопрос задан 7 лет назад

< >

Помогите,пожалуйста!!! Не могу значения в промежутке найти
Cos2x-Sin^2x=0,25 [P/2;3P]

Ответы

Ответ дал: Helper211

0

Ответ: $frac{pi}{6} ,frac{7pi}{6} ,frac{11pi}{6}, frac{13pi}{6} ,frac{17pi}{6}$

Пошаговое объяснение:

$cos2x-sin^2x=0.25\$

Применим формулу двойного угла для косинуса:

$cos(2t)=1-2sin^2t$

Тогда:

$cos2x-sin^2x=0.25\1-2sin^2x-sin^2x=0.25\1-3sin^2x=0.25\3sin^2x=1-0.25=0.75\sin^2x=0.25\sinx =pm 0.5$

1 случай:

$sinx=frac{1}{2} \x=frac{pi}{6}+2pi k, kin Z \\x=frac{5pi}{6}+2pi k, kin Z \$

2 случай:

$sinx=-frac{1}{2} \x=frac{11pi}{6}+2pi k, kin Z \\x=frac{7pi}{6}+2pi k, kin Z \$

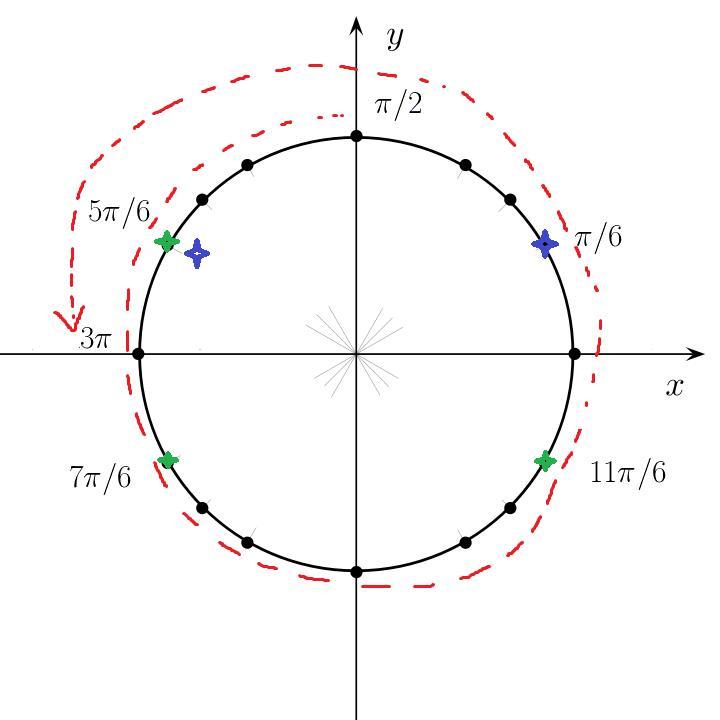
На рисунке видно, что

$frac{5pi}{6} +pi=frac{11pi}{6} \frac{pi}{6} +pi=frac{7pi}{6} \$

Объединив ответы, получим окончательное решение:

$x=frac{pi}{6}+pi k, kin Z \\x=frac{5pi}{6}+pi k, kin Z \$

На рисунке указан промежуток $[frac{pi}{2};3pi]$ и корни уравнения в этом промежутке (синими звездочками обозначены корни, к которым надо прибавить $2pi$ , поскольку мы проходим круг второй раз):

$frac{pi}{6} ,frac{7pi}{6} ,frac{11pi}{6}, frac{pi}{6}+2pi ,frac{5pi}{6}+2pi$

Или:

$frac{pi}{6} ,frac{7pi}{6} ,frac{11pi}{6}, frac{13pi}{6} ,frac{17pi}{6}$

Приложения:

Похожие вопросы

Английский язык

1 год назад

помогите пожалуйста, очень прошу, срочно!!! :(((((

Английский язык

1 год назад

поставь в пропуски подходящие слова и переведи ...the bird in the cage? no, it isn t

География

2 года назад

ДАЮ 45 БАЛЛОВ!!! Дать характеристику озера Байкал по плану: 1. Географическое положение 2. Происхождение озерной котловины. 3. Особенности стока. 4. Особенности минерального состава воды. 5.

Қазақ тiлi

2 года назад

Жәдігерлер саны қанша? Реттік сан есімі бар сөйлемді көрсет. Көшпенділер туралы жеті кітап оқыдым. ХХ ғасыр болса да әлі көшіп жүрген халықтар бар екен. Сынған үш арбаның екеуі жөнделді. 4 айдан соң

Математика

8 лет назад

Придумать 5 примеров на умножение в столбик и ОФОРМИТЬ НЕСТАНДАРТНО. Программа 3 класс, главное в задании оформление.

Физика

8 лет назад

к источнику тока, эдс которого составляла 4 в , а внутреннее сопротивление 1 ом,присоединили резистор с сопротивлением 4ом , найти силу тока

Математика

9 лет назад

Увеличь каждое число в4 раза: 9, 13, 15, 24, 18. Уменьши каждое число в 4 раза: 40, 76, 52, 60, 84.

История

9 лет назад

заполнить таблицу по истории на тему средневековая литература