• Предмет: Геометрия
  • Автор: savrandima2006
  • Вопрос задан 7 лет назад
< >

Помогите решить задачу

Приложения:

Ответы

Ответ дал: UluanaV
0

Ответ:

9

Объяснение:

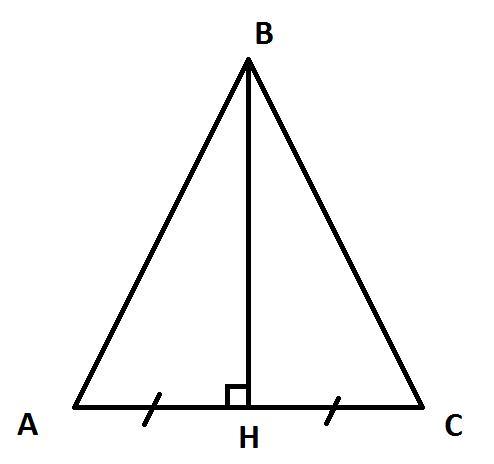
Пусть дан равносторонний треугольник АВС.

AB=BC=AC=6sqrt{3} (по условию).

Пусть ВН - высота в ΔАВС. Высота в равностороннем треугольнике также является и медианой. Значит:

AH=HC=frac{AC}{2}=frac{6sqrt{3} }{2}=3sqrt{3}

ΔАВН - прямоугольный. По теореме Пифагора найдем ВН:

BH=sqrt{AB^2-AH^2}=sqrt{(6sqrt{3})^2-(3sqrt{3})^2 } =sqrt{36*3-9*3}=sqrt{3(36-9)}=sqrt{3*27}=sqrt{3*3*9}=sqrt{3*3}*sqrt{9}=3*3=9

Ответ: ВН=9

Приложения:
Похожие вопросы
Английский язык
2 года назад
Помогите пожалуйста ответить на вопросы по этому тексту. 5 . Read one text more carefully, then answer the questionswith a partner who read the other text. 1 When were Milton and Hetty born? 2 What
Русский язык
2 года назад
Помогите пожалуйста,очень срочно!!!!!
Математика
2 года назад
Известно, что а<b< с. Укажи а. наименьшую дробь: ba1 a b. c b а а Ь​
Русский язык
2 года назад
Какими частями речи и членами предложения являются выделенные слова? 1) дежурный врач подошёл к больному. 2) нет отдыха моему больному сердцу!
Химия
8 лет назад
найти молекулярную формулу вещества содержащего 75%углерода и 25% водорода относительная плотность водорода 8
Химия
8 лет назад
Помогите пожалуйста срочно по химии! 2. Напишите уравнения реакций, при помощи которых можно осуществить следующие превращения: С → СН4 → СН3С1 → СН3ОН → СН3 – СОО – СН3 . 3. Распределите
Биология
9 лет назад
Мозоль - это скопление : а) крови б)лимфы в)межклеточного вещества
Информатика
9 лет назад
Ссылка на файл или папку. 5 букв.