Висоти паралелограма 6см і 8 см, а кут між ними 30º. Знайдіть площу паралелограма.

Задача: Высоты параллелограмма 6 и 8 см, а угол между ними 30º. Найти площадь параллелограмма.

Решение:

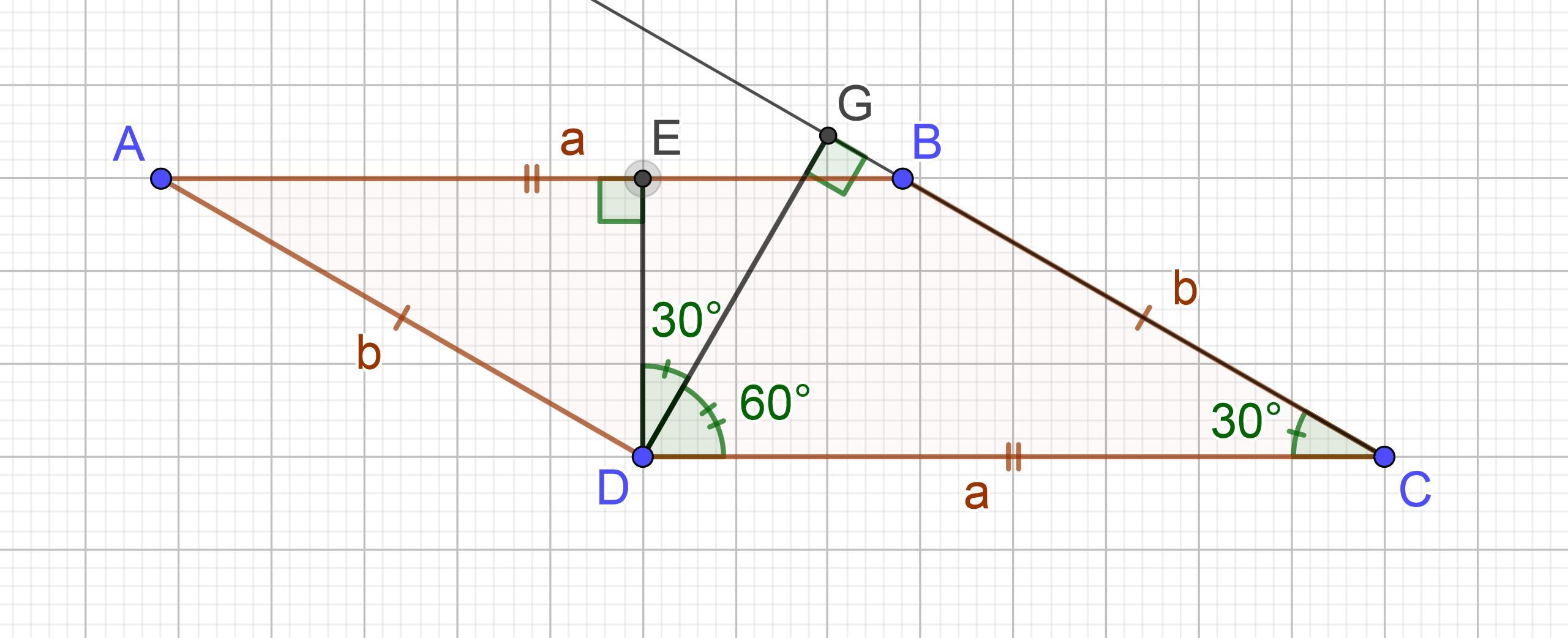
Обозначим параллелограмм ABCD, высоты DE = 6 см и DG = 8 см, ∠EDG = 30°.

∠EDC = 90°  ⇒  ∠GDC = 90°−∠EDG = 90°−30° = 60°  ⇒  

⇒  ∠GCD = 90°−∠GDC = 90°−60° = 30°

Катет, лежащий напротив угла 30°, равен половине гипотенузы :

DC = DG·2 = 8·2 = 16 (см)

Подставим значения в формулу площади параллелограмма:

S = a·hₐ = DC·ED = 16·6 = 96 (см²)

Ответ:

Площадь параллелограмма равна 96 см².