Предмет: Алгебра
Автор: xgxjf
Вопрос задан 7 лет назад

< >

помогите напишите на листочке даю Макс.баллов

Приложения:

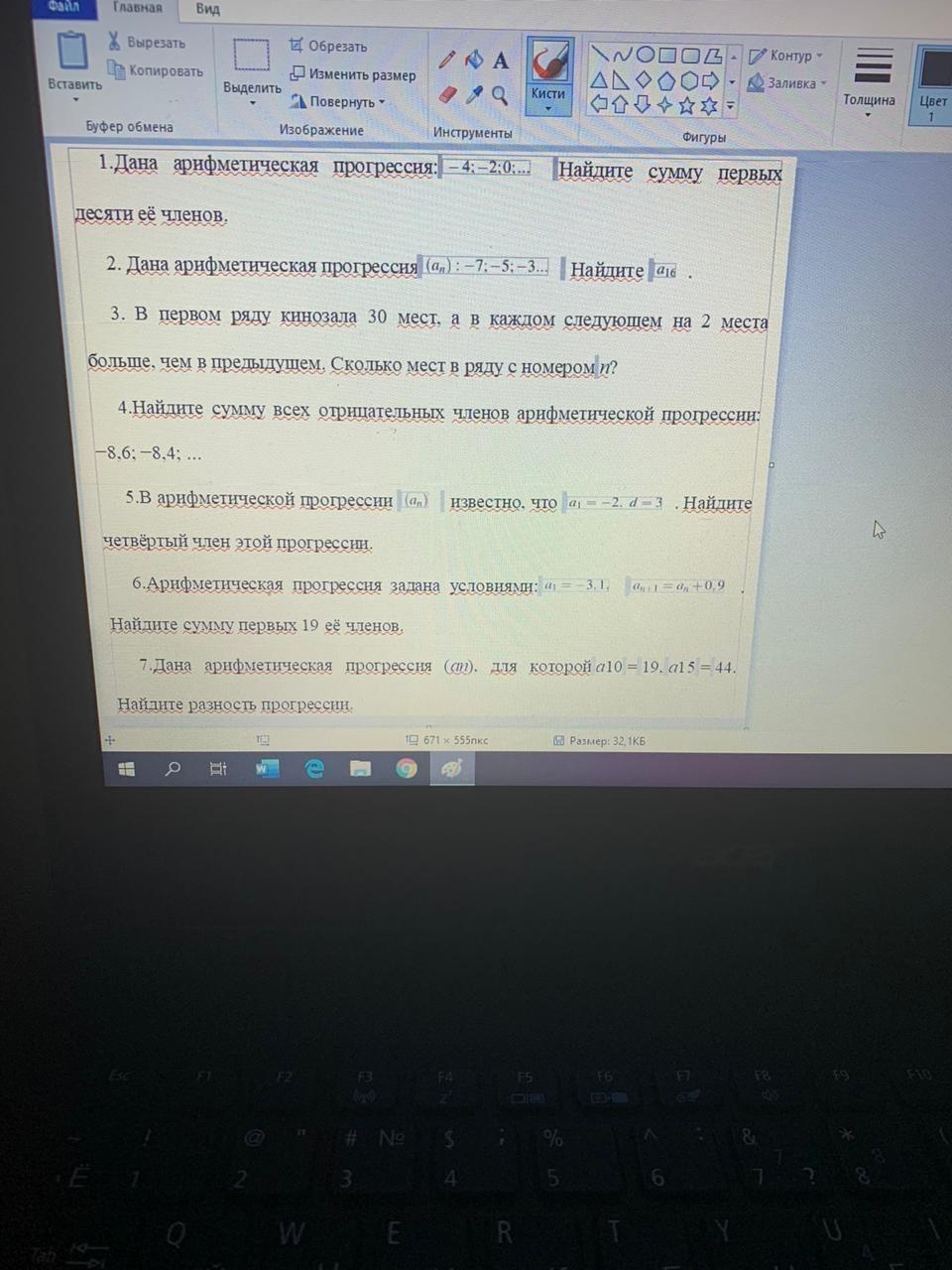
Ответы

Ответ дал: nktselepov

$a_1=-4; d=-2-(-4)=2\S_n=frac{2a_1+d(n-1)}{2} *n\S_{10}=frac{2*(-4)+2(10-1)}{2}*10= 10*5=50$

$a_1=-7; d=-5-(-7)=2\a_n=a_1+d(n-1)\a_{16}=-7+2(16-1)=23$

Для решения задачи воспользуемся арифметической прогрессии

Здесь

$a_1=30, d=2$

$a_n=a_1+d(n-1)\a_n=30+2(n-1)\a_n=30+2n-2\a_n=28+2n$

$a_1=-8,6, d=-8,4-(-8,6)=0,2\a_n=a_1+d(n-1)\-8,6+0,2(n-1)<0\-8,6+0,2n-0,2<0\0,2n<8,8\n<44$

$a_{44}=-8,6+0,2(44-1)=0$ , значит прогрессия имеет 43 отрицательных члена. Найдем сумму первых 43 членов данной прогрессии

$S_n=frac{2a_1+d(n-1)}{2} *n\S_{43}=frac{2*(-8,6)+0,2(43-1)}{2} *43=-189,2$

$a_1=-2, d=3\a_n=a_1+d(n-1)\a_4=-2+3(4-1)=7$

$a_{n+1}=a_n+0,9$ , значит d=0,9

$a_1=-3,1$

$S_n=frac{2a_1+d(n-1)}{2} *n\S_{19}=frac{2*(-3,1)+0,9(19-1)}{2} *19=95$

$a_n=a_1+d(n-1)$ ⇒

$a_{10}=a_1+9d\a_{15}=a_1+14d$ , значит

$19=a_1+9d\44=a_1+14d$

Вычитаем из второго уравнения первое, получим

$25=5d\$ , отсюда

$d=5$

Похожие вопросы

Русский язык

1 год назад

Выбери из скобок подходящие слова,чтобы получились

Русский язык

1 год назад

помогите зделать 128 упражнение по русскому языку

Математика

2 года назад

запиши все числа от 4504 до 4498

Математика

2 года назад

(-1)^4-(-1)^5 помогите

Алгебра

8 лет назад

Разложите пожалуйста на множители Заранее ОГРОМНОЕ СПАСИБО!!!

Физика

8 лет назад

Льдина получила 10, 5 МДж тепла в результате чего лёд нагрелся на 10*C. Чему равна масса льдины

Химия

9 лет назад

Помогите пожалуйста вычислите объём этилена полученного при гидрировании 20 л ацетилена содержащего 10 % примеси

Математика

9 лет назад

Квадрат и прямоугольника имеют равные площади,соседние стороны прямоугольника равны 3см и 12см.Найти пириметр кавадрата