Рассчитай расстояние вершины куба до диагонали куба, которая не проходит через эту вершину, если ребро куба — 12 см.

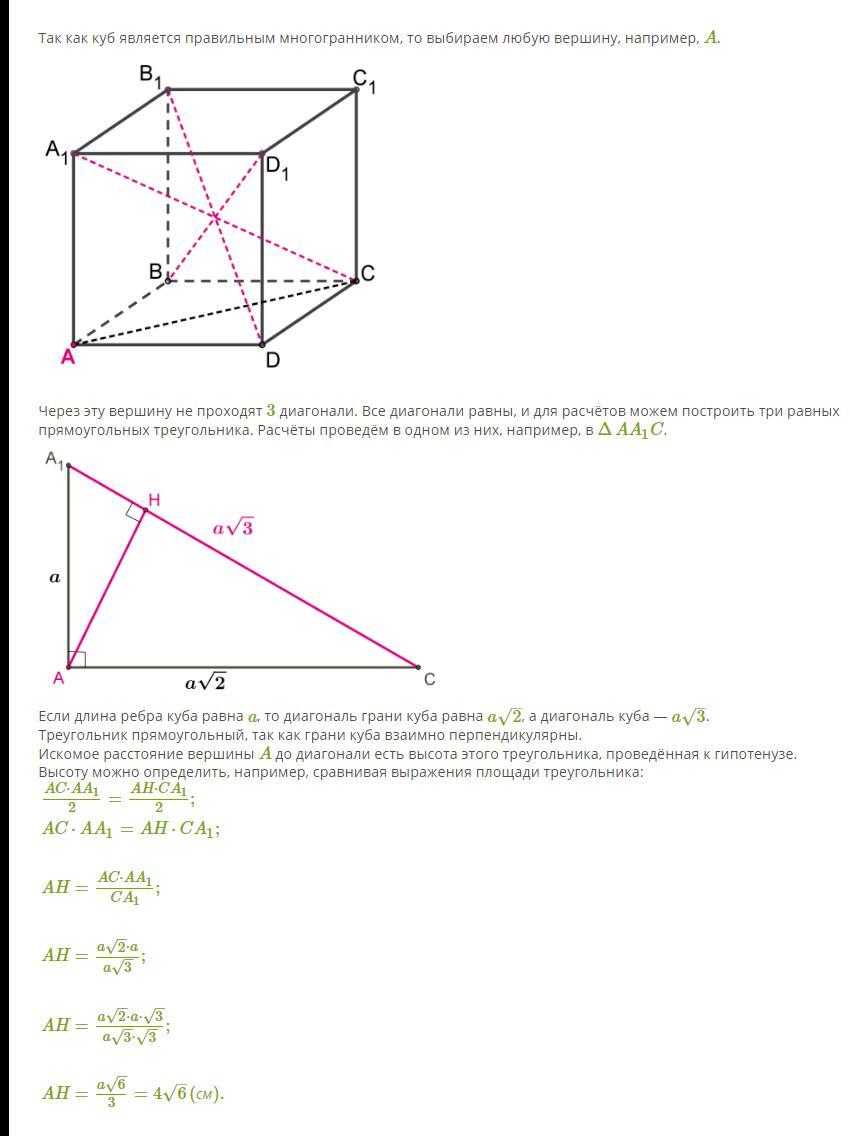
Так как куб является правильным многогранником, то выбираем любую вершину, например, A.

Через эту вершину не проходят 3 диагонали. Все диагонали равны, и для расчётов можем построить три равных прямоугольных треугольника. Расчёты проведём в одном из них, например, в ΔAA1C.

Если длина ребра куба равна a, то диагональ грани куба равна a2–√, а диагональ куба — a3–√.

Треугольник прямоугольный, так как грани куба взаимно перпендикулярны.

Искомое расстояние вершины A до диагонали есть высота этого треугольника, проведённая к гипотенузе. Высоту можно определить, например, сравнивая выражения площади треугольника: