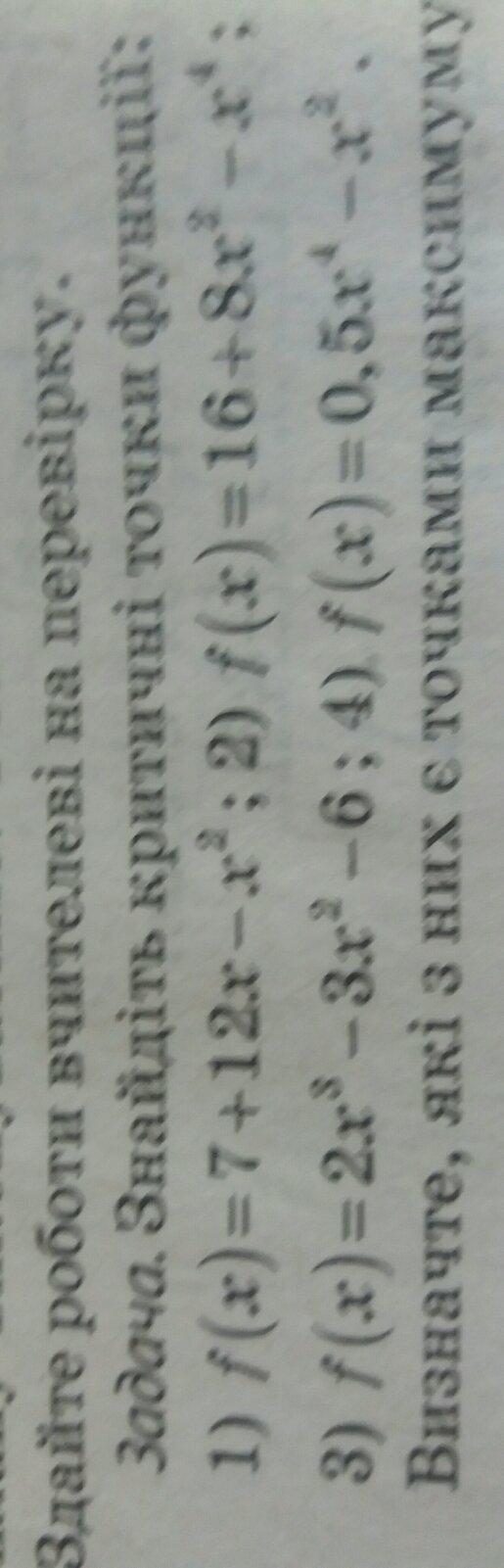Ответы
Ответ:
Объяснение: Точки функції є критичними, якщо похідна в цих точках =0. Критичні точки є точками max, коли похідна в цій точці змінює знак з + на -.
1) f'(x)=-2x+12, -2x+12=0, x=6
f'(5)=-2·5+12=2 +
f'(7)=-2·7+12=-2 -
Точка з абсцисою x=6 є точкою max
2)f'(x)=-4x³+8x, -4x³+8x=0, 4x·(2-x²)=0, 4x·(√2-x)·(√2+x)=0
x₁=0, x₂=√2, x₃=-√2 - критичні точки
f'(-2)=-4·(-2)³+8·(-2)=32-16=16 +
f'(-1)=-4·(-1)³+8·(-1)=4-8=-8 -
f'(1)=-4·1³+8·1=+4 +
f'(3)=-4·3³+8·3=-108+24=-84 -
Точки з абсцисами x₃=-√2 і x₂=√2 є точками max
3) f'(x)=6x²-6x, 6x²-6x=0, 6x(x-1)=0
x₁=0, x₂=1 критичні точки.
f'(-1)=6·(-1)²-6·(-1)=6+6=12 +
f'(1/2)=6·(1/2)²-6·(1/2)=3/2-3=-3/2 -
f'(5)=6·5²-6·5=150-30=120 +
Точка з абсцисою x₁=0 є точкою max
4) f'(x)= 2x³-2x, 2x³-2x=0, 2x(x²-1)=0, 2x(x-1)(x+1)=0
x₁=0, x₂=1, x₃=-1 - критичні точки
f'(-4)=2·(-4)³-2·(-4)=-128+8=-120 -
f'(-1/2)=2·(-1/2)³-2·(-1/2)=-1/4+1=3/4 +
f'(1/2)=2·(1/2)³-2·(1/2)=1/4-1=-3/4 -
f'(2)=2·2³-2·2=16-4=12 +
Точка з абсцисою x₁=0 є точкою max