Была куплена краска для окраски боковых поверхностей цилиндрических брёвен длиной 1 м и радиусом 7,5 см.
Затем было решено из цилиндрических брёвен выпилить брёвна в форме прямоугольного параллелепипеда с отношением сторон 3:4 и покрасить их боковые поверхности.
Сколько процентов от количества купленной краски останутся неиспользованными?
(Введи ответ округлённым до целых процентов.)

Ответы

Ответ дал: White0w1

Ответ:

неиспользованными останутся 11 % купленной краски.

Приложения:

akaman32: перед тем, как выкладывать копию решения с какого-то источника, вы хотя бы убедитесь, что исходные данные совпадают.

Ответ дал: akaman32

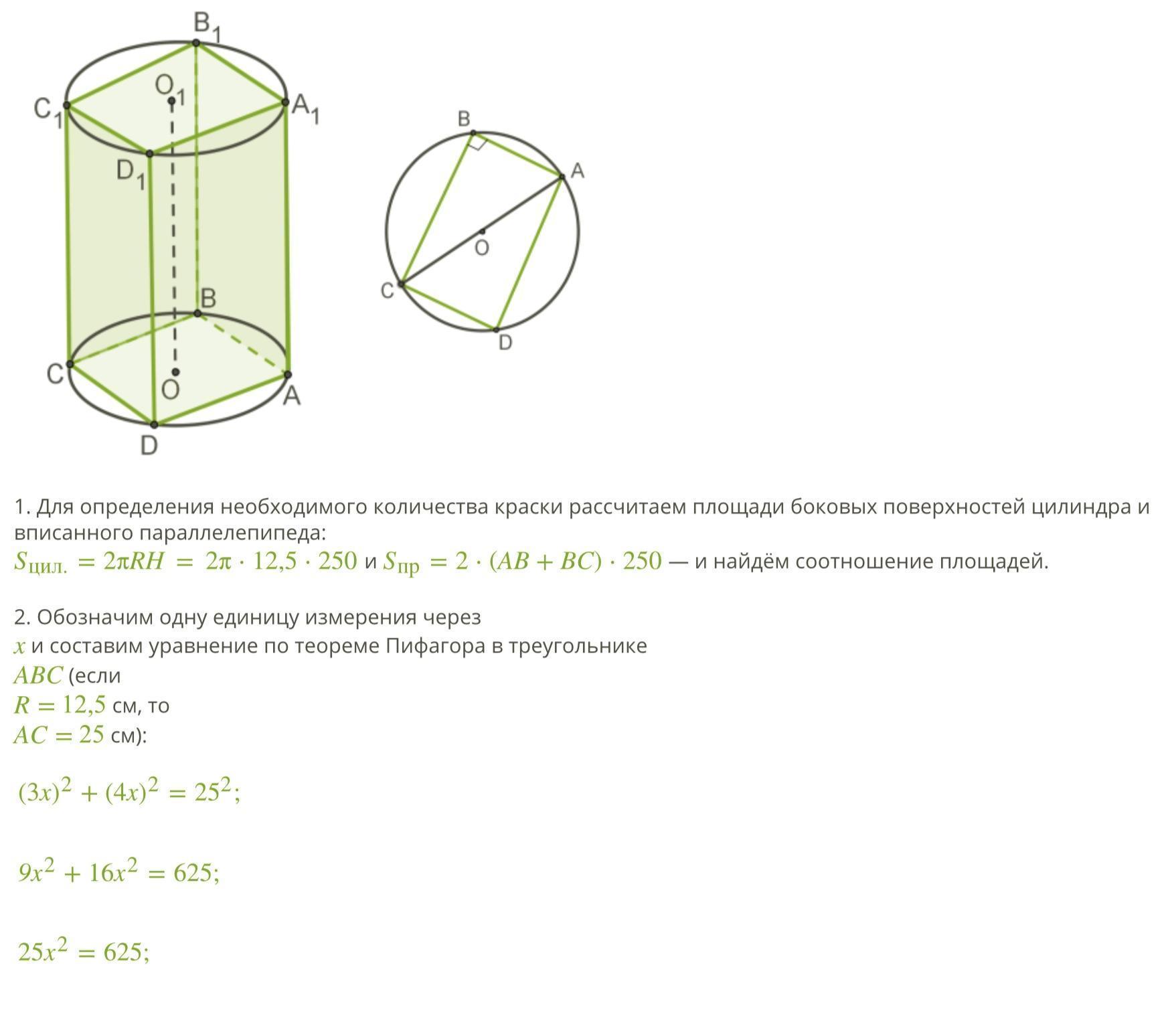
Ответ:

11%

Пошаговое объяснение:

1) Найдём площадь боковой поверхности бревна:

$S_{1} =2*\pi *R*l$ , где R - радиус бревна, l - его длина

(Все единицы приведем к сантиметрам)

$S_{1} \approx 2*3.14*7.5*100=4710 (cm^{2} )$

2) Найдем длину и ширину прямоугольного сечения бревна.

Диагональ такого сечения равна диаметру D исходного бревна, а так как нам известно соотношение сторон прямоугольника, то, обозначив их за 3х и 4х, получаем выражение (по т. Пифагора):

$D=\sqrt{(3x)^{2} +(4x)^{2} } =\sqrt{25x^{2} } =5x$

D=2R=5x ⇒ 5x=15 ⇒ x=3

Значит длина прямоугольного сечения: a = 4х = 12 см;

а ширина прямоугольного сечения: b = 3х = 9 см.

Тогда площадь поверхности такого бревна будет:

$S_{2}=2*(a+b)*l$

S₂ = 2*(12+9)*100 = 4200 см²

Т.к. S₁ = 100%, а S₂ = ?%, то составим пропорцию:

$\frac{S_{1}}{100} =\frac{S_{2}}{p_{2}}$ , где р₂ - процентное значение площади прямоугольного параллелепипеда относительно площади цилиндрического бревна.