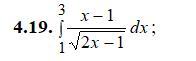Помогите ,пожалуйста, вычислить интеграл. Нужно полное решение

Приложения:

Ответы

Ответ дал: Helper211

Ответ: $frac{sqrt{5}+1 }{3}$

Пошаговое объяснение:

$int {frac{x-1}{sqrt{2x-1}}dx }=int{frac{x}{sqrt{2x-1}}dx}-int{frac{1}{sqrt{2x-1}}dx}$

Первый интеграл:

$int{frac{x}{sqrt{2x-1}}dx}\\t=2x-1\\2x=t+1\\x=frac{t+1}{2}\\ dx=frac{1}{2} dt\\int{frac{x}{sqrt{2x-1}}dx}=int {frac{(frac{t+1}{2} )(frac{1}{2} dt)}{sqrt{t} } }=int {frac{t+1}{4sqrt{t} } dt}=int {frac{t}{4sqrt{t} } dt}+int {frac{1}{4sqrt{t} } dt}=\\frac{1}{4} int {t^{frac{1}{2} }dt}+frac{1}{4}int {t^{-frac{1}{2} }dt}=frac{t^{frac{3}{2} }}{6} +frac{sqrt{t} }{2} +C=frac{(2x-1)^{frac{3}{2} }}{6} +frac{sqrt{2x-1} }{2} +C$

Второй интеграл решается аналогичной заменой $t=2x-1$ :

$int{frac{1}{sqrt{2x-1}}dx}=int{frac{dt}{2sqrt{t} } }=frac{1}{2} int {t^{-frac{1}{2} }dt}=sqrt{t} +C=sqrt{2x-1} +C$

Итак,

$int {frac{x-1}{sqrt{2x-1}}dx }=int{frac{x}{sqrt{2x-1}}dx}-int{frac{1}{sqrt{2x-1}}dx}=frac{(2x-1)^{frac{3}{2} }}{6} +frac{sqrt{2x-1} }{2} -sqrt{2x-1}+C$

Вычислим определенный интеграл:

$left[ frac{(2x-1)^{frac{3}{2} }}{6} +frac{sqrt{2x-1} }{2} -sqrt{2x-1}right]bigg| limits^3_1=left[ frac{(2cdot 3-1)^{frac{3}{2} }}{6} +frac{sqrt{2cdot 3-1} }{2} -sqrt{2cdot 3-1}right]-\\left[ frac{(2cdot 1-1)^{frac{3}{2} }}{6} +frac{sqrt{2cdot 1-1} }{2} -sqrt{2cdot 1-1}right]=left[ frac{5sqrt{5} }{6} +frac{sqrt{5} }{2} -sqrt{5} right]-left[ frac{1 }{6} +frac{1 }{2} -1 right]=frac{sqrt{5}}{3} +frac{1}{3} =frac{sqrt{5}+1 }{3}$