Предмет: Математика
Автор: AL1KO
Вопрос задан 7 лет назад

y''+7y' = 3e^2x помогите решить, вроде диф уравнение это

и если сможете решите 3 задачу

Приложения:

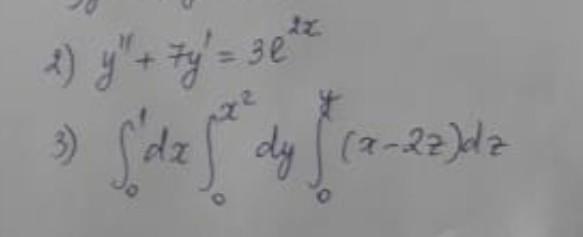
Ответы

Ответ дал: NNNLLL54

$2); ; ; y''+7y'=3e^{2x}\\a); ; k^2+7k=0; ; ,; ; k(k+7)=0; ; ,; ; k_1=0; ,; k_2=-7\\y_{oo}=C_1+C_2cdot e^{-7x}\\b); ; f(x)=3e^{2x}; ; to ; ; alpha =2ne 0ne -7; ; to ; ; r=0\\y_{chastn.}=Ae^{2x}cdot x^0=Ae^{2x}\\y'=2Ae^{2x}\\y''=4Ae^{2x}\\y''+7y'=4Ae^{2x}+14Ae^{2x}=3e^{2x}; ; ,qquad 18Ae^{2a}=3e^{2x}\\18A=3; ; to ; ; A=frac{1}{6}\\y_{chastn.}=frac{1}{6}cdot e^{2x}\\c); ; y_{on}=C_1+C_2e^{-7x}+frac{1}{6}cdot e^{2x}$

$3)int limits _0^1, dx; intlimits^{x^2}_0, dy; intlimits^{y}_0, (x-2z),dz=intlimits^1_0, dx; intlimits^{x^2}_0, dy; Big(xz-frac{2z^2}{2}Big)Big|_0^{y}=\\=intlimits^1_0, dx; intlimits^{x^2}_0, dy; Big (xy-y^2Big)=intlimits^1_0, dx; intlimits^{x^2}_0, Big (xy-y^2Big), dy=\\=intlimits^1_0, dx; Big(xcdot frac{y^2}{2}-frac{y^3}{3}Big)Big|_0^{x^2}=intlimits^1_0, Big(frac{x^5}{2}-frac{x^6}{3}Big), dx=Big(frac{x^6}{12}-frac{x^7}{21}Big)Big|_0^1=$