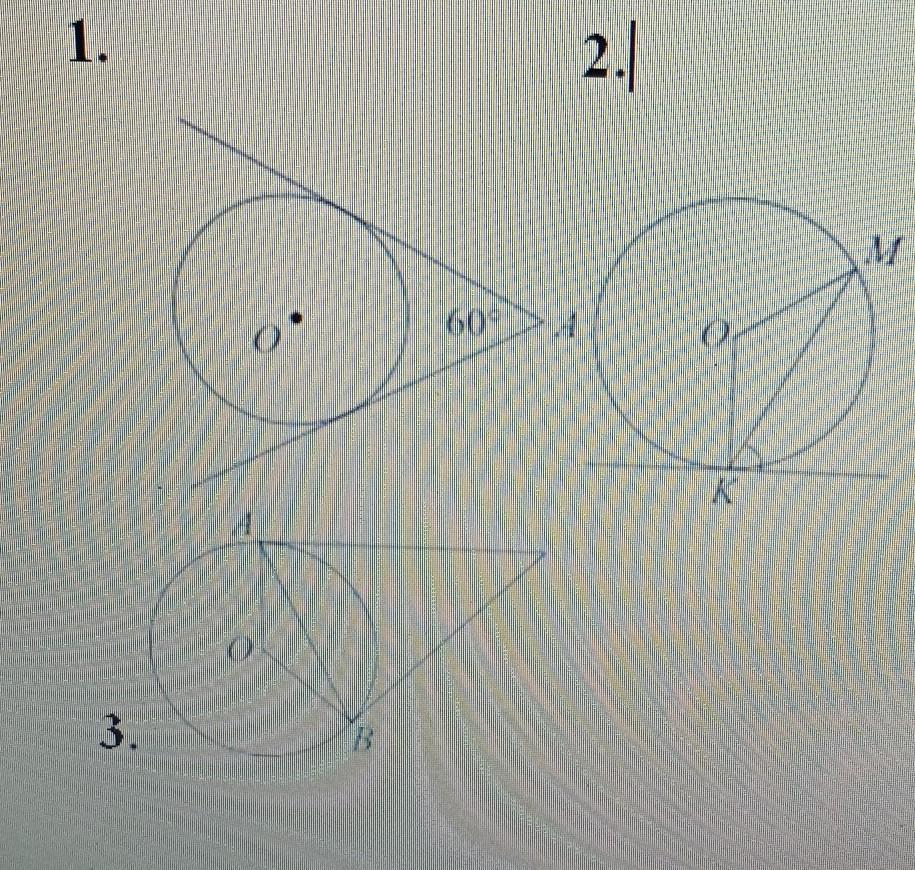
1.Из точки А проведены две касательные к окружности с центром к точке О. Найдите радиус окружности, если угол между касательными равен 60°,а расстояние от точки А до точки О равно 16.
2. Прямая касается окружности точке К. Точка О - центр окружности. Хорда КМ образует с касательной угол, равный 62°. Найдите величину угла ОМК. Ответ дайте в градусах.
3. Касательные в точках А и В к окружности с центром О пересекаются под углом 14 °. Найдите угол АВО. Ответ дайте в градусах.
Помогите пожалуйста❤️за ответ дам 65 баллов. Решить нужно через дано. Прикрепила фото с чертежами.
Приложения:
Ответы
Ответ дал:
0
Ответ:
1. Расстояние от центра окружности до точки, из которой проведены две касательные, делит угол A пополам. Значит угол HAO равен 30 градусам. Проведем радиус от точки O в точку касания окружности с касательной. Радиус, проведенный из центра окружности к точке касания является перпендикуляром к касательной. Получается прямоугольный треугольник HAO. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов половине гипотенузы. OA - гипотенуза
OH=1/2*6
OH=3
OH-радиус окружности
Ответ:R=3
2.28 градусов
3.7
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад