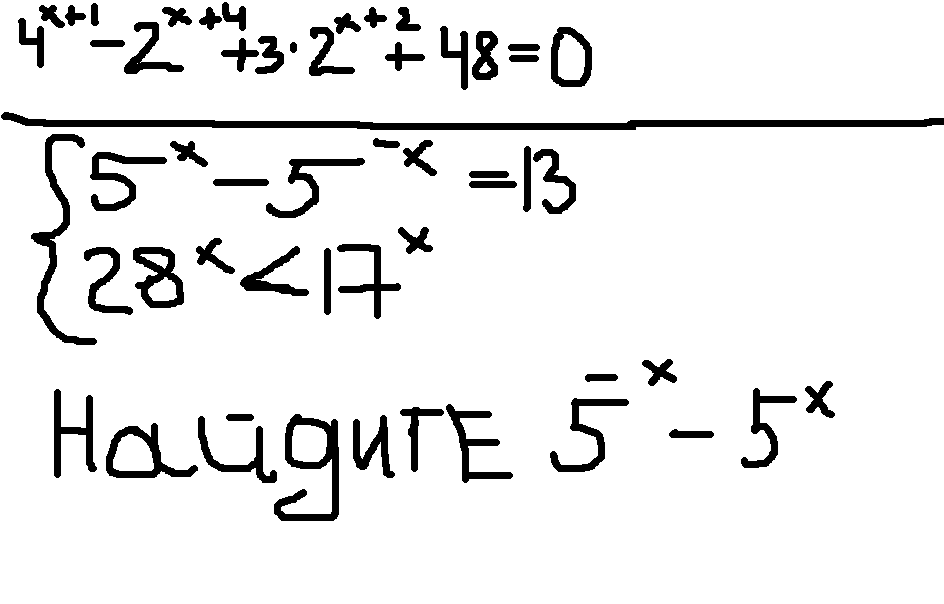Предмет: Алгебра
Автор: emilyoops
Вопрос задан 10 лет назад

Помогите решить сложные показательные неравенства.
Нужно полное решение.

Приложения:

Ответы

Ответ дал: Матов

$4^{x+1}-2^{x+4}+3*2^{x+2}+48=0\ 4^{x}*4-16*2^{x}+12*2^{x}+48=0\ 4*2^{2x}-4*2^{x}+48=0\ zamena\ 2^{x}=t\ 4t^2-4t+48=0\ D<0$
нет решений!!!!

$5^x-5^{-x}=13\ 28^x<17^x\ \ x<0\ 5^x-frac{1}{5^x}=13\ 5^{2x}-13*5^x-1=0\ 5^x=a\ a^2-13a-1=0\ D=169+4*1*1=sqrt{173}\ a=frac{13+sqrt{173}}{2}\ a=frac{13-sqrt{173}}{2}\ \ 5^x=frac{13+sqrt{173}}{2} 5^x-5^{-x}=13, 28^x<17^x$
из этого следует что система не совместима,так как из первого условию следует что x>0

Похожие вопросы

Русский язык

2 года назад

Синтаксический разбор предложения со схемой Из погреба то плесенью пахнет, то сыростью, то мохом. Чем является (то)? Местоимением, частицей или суффиксом?!

Русский язык

2 года назад

Слово:Сестра, морфологический разбор

Алгебра

7 лет назад

Помогите решить пожалуйста, очень срочно

Алгебра

7 лет назад