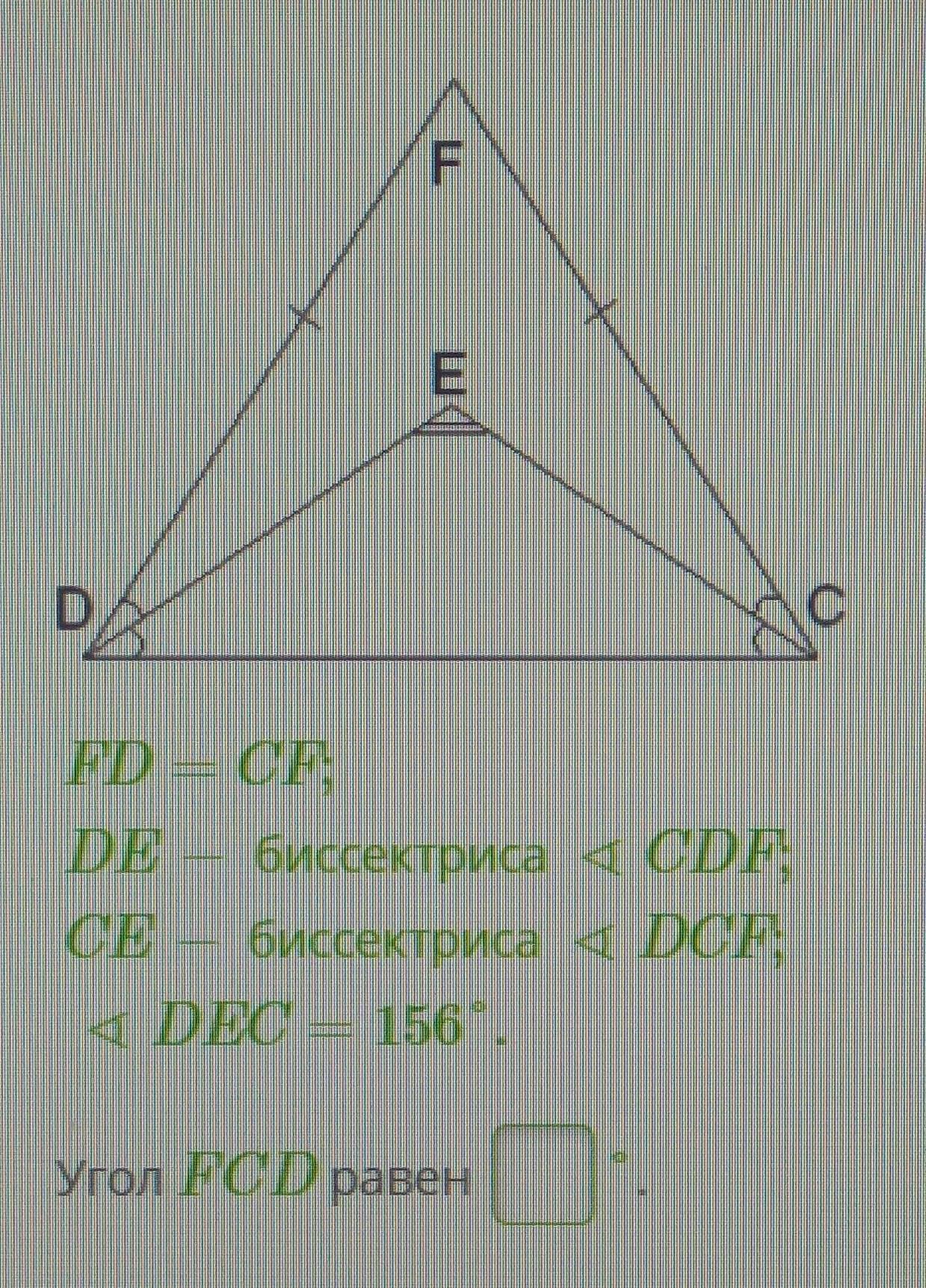
Условие задания.
FD = CF
DE – биссектриса угла CDF
СЕ – биссектриса угла DCF
Угол DEC – 156.
Угол FCD равен
Помогите пожалуйста, срочно:(​

Дано:

FD = CF.

DE - биссектриса.

CE - биссектриса.

∠DEC = 156˚.

Найти:

∠FCD.

Решение.

Т.к. FD = CF => △BFC - равнобедренный.

=> ∠CDE = ∠DCE, по свойству.

180° - 156° = 24° - сумма ∠CDE и ∠DCE.

=> ∠CDE = ∠DCE = 24° : 2 = 12˚.

∠FCD = ∠DCE * 2 = 12° * 2 = 24˚. (т.к. CE - биссектриса).

Ответ: 24°.