Помогите пожалуйста решить срочно! Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 65, длина хорды AB равна 50. Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.​

Ответ:

125 ед.

Объяснение:

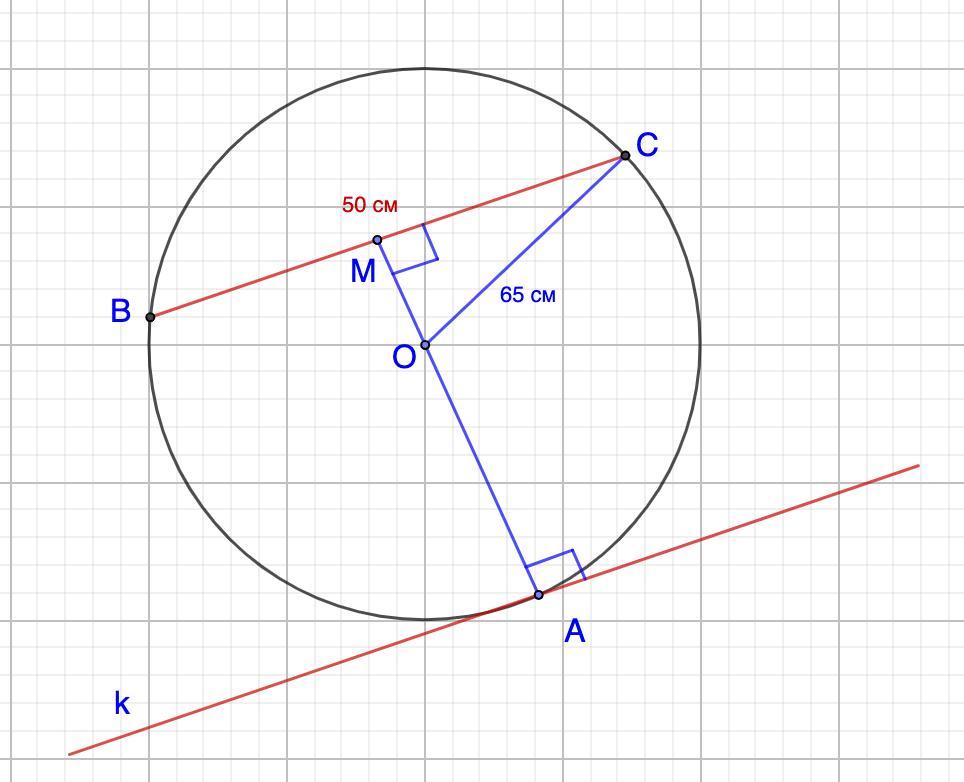
Дано: Окр.OR

R=65;

BC=50 - хорда

k ║ BC - касательная

Найти: АМ

Решение:

ОА⊥k (радиус перпендикулярен касательной)

ВС║k ⇒ BC⊥AM

⇒ BM=MC (радиус перпендикулярный хорде точкой пересечения делит ее пополам)

То есть ВМ=МС=50:2=25

Рассмотрим ΔОМС - прямоугольный.

МС=25

ОС=65

По теореме Пифагора:

АМ=ОМ+ОА=ОМ+R=60+65=125