Пожалуйста, помогите решить задачу. Периметр правильного четырехугольника, вписанного в окружность, равен 16 см. Найдите периметр треугольника, вписанного в эту же окружность.

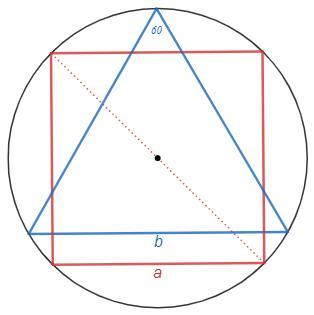
Правильный четырехугольник - квадрат.

a - сторона квадрата

a =Pк/4 =16/4 =4

Диагональ квадрата - диаметр описанной окружности.

2R =a√2 =4√2

b - сторона равностороннего треугольника

По теореме синусов

b/sin60 =2R => b =4√2 *√3/2 =2√6

Pт =3b =6√6 (см)

Или

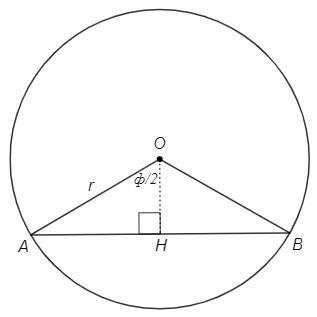
Найдем длину хорды L по радиусу R и центральному углу Ф.

AOB=Ф, OA=OB=R

OH - высота, медиана, биссектриса

AB=2AH, AOH=Ф/2, sin(AOH)=AH/OA

L =AB =2R sin(Ф/2)  

Вершины равностороннего треугольника делят окружность на три равные дуги.

Фт =360/3

Вершины квадрата делят окружность на четыре равные дуги.

Фк =360/4  

Lт/Lк =sin(Фт/2) / sin(Фк/2) =sin60/sin45 =√3/√2

Pт/Pк =3Lт/4Lк

Pт =16 *3/4 *√3/√2 =6√6 (см)