1.Стороны треугольника соответственно равны 8 см, 9 см и 10 см. Найди косинус большего угла треугольника.


2.Дан треугольник ABC.


AC= 26,4 см;


Смотреть скриншоты


∢ B= 45°;

∢ C= 60°.


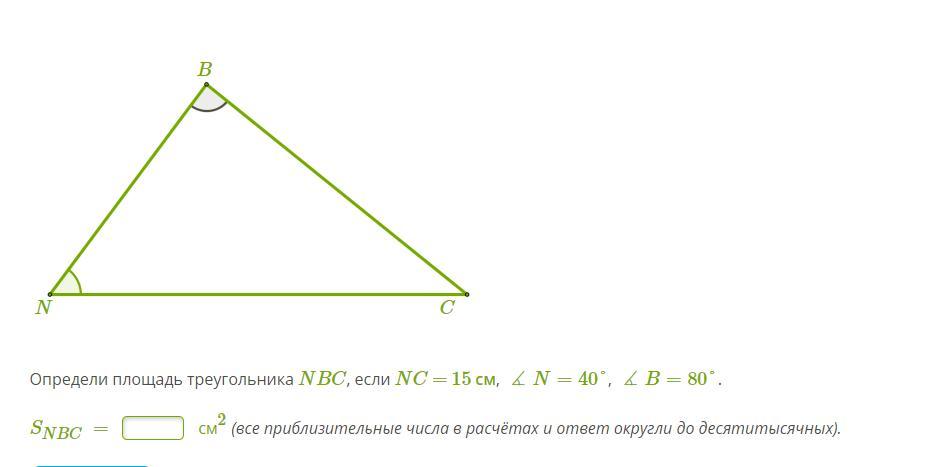
3.Определи площадь треугольника NBC, если NC = 15 см, ∡N=40°, ∡B=80°.