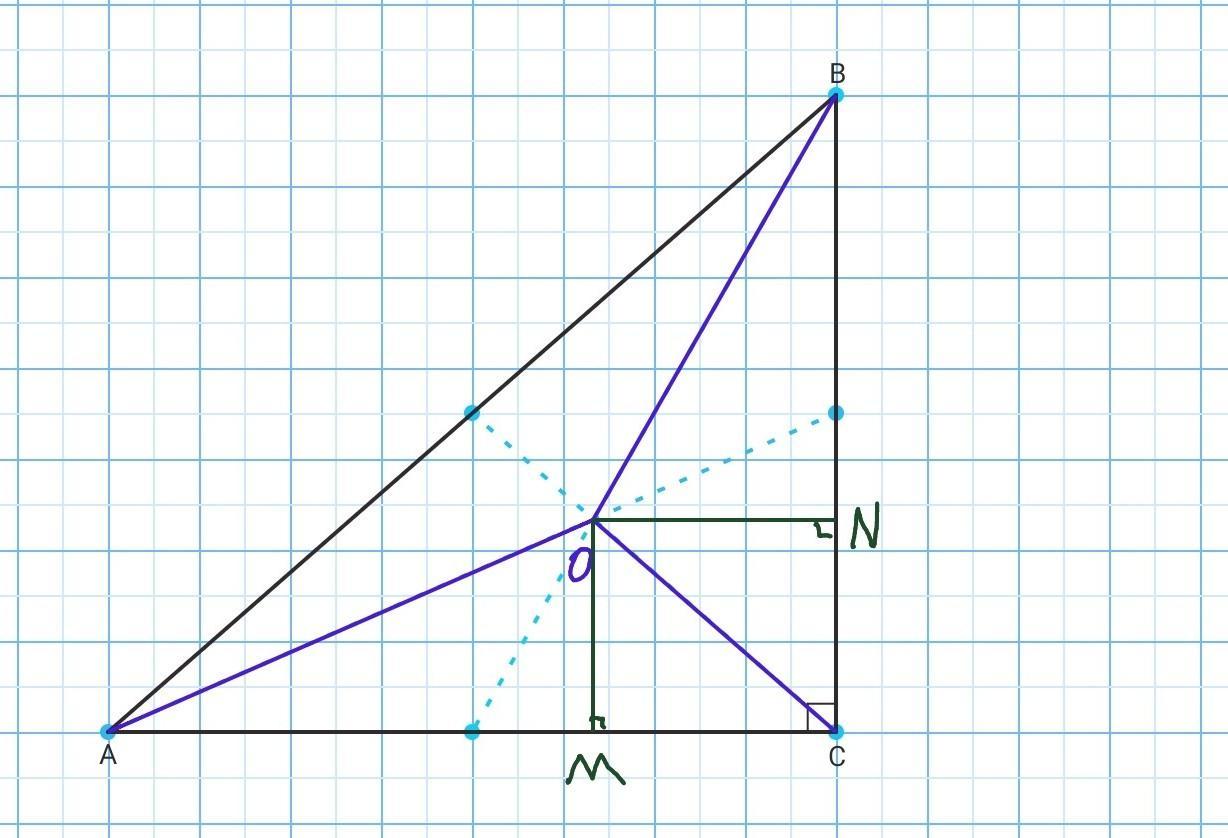
Внутри прямоугольного треугольника АВС (C 90 °) взято точку O так, что треугольники ОАВ, ОВС и ОАС - равновеликие. Найти длину отрезка ОС, когда известно, mo OA² + OB² = d?

Ответы

Ответ дал: ReMiDa

Ответ:

ОС=

$\ \sqrt{ \dfrac{d}{5} }$

Объяснение:

Проведём перпендикуляры ОМ⟂АС и ON⟂BC. Площадь прямоугольного треугольника АВС:

$S = \dfrac{1}{2} \times AC \times BC$

Так как точка О разбивает треугольник ABC на 3 равновеликих треугольника то площадь треугольника АОС будет равна:

$S(AOC) = \dfrac{1}{3} \times S(ABC) = \dfrac{1}{3 } \times \dfrac{1}{2} \times AC \times BC = \dfrac{1}{6} \times AC \times BC$

С другой стороны:

$S(AOC) = \dfrac{1}{2} \times AC \times OM$

Получаем:

$\dfrac{1}{6} \times AC \times BC = \dfrac{1}{2} \times OM \times AC \\ \\ BC = 3OM \\ \\ OM = \dfrac{1}{3} BC$

Аналогично получаем, что

$ON = \dfrac{1}{3} AC$

Так как ONMC - прямоугольник, то NC=OM, MC=ON.

$AM = AC - MC = AC - \dfrac{1}{3} AC = \dfrac{2}{3} AC$

Аналогично:

$BN = \dfrac{2}{3} \times BC$

Воспользовавшись теоремой Пифагора найдём гипотезы треугольников АОМ, BON, COM:

${OA}^{2} = {AM}^{2} + {OM}^{2} = \dfrac{4}{9} {AC}^{2} + \dfrac{1}{9} {BC}^{2} \\ \\ {OB}^{2} = {BN}^{2} + {ON}^{2} = \frac{4}{9} {BC}^{2} + \frac{1}{9} {AC}^{2} \\ \\ {OC}^{2} = {OM}^{2} + {MC}^{2} = \frac{1}{9 } {BC}^{2} + \frac{1}{9} {AC}^{2}$

Отсюда следует:

${OA}^{2} + {OB}^{2} = \dfrac{4}{9} {AC}^{2} + \dfrac{1}{9} {BC}^{2} + \dfrac{4}{9} {BC}^{2} + \dfrac{1}{9} {AC}^{2} = \\ \\ = \dfrac{5}{9} {AC}^{2} + \dfrac{5}{9} {BC}^{2} = 5( \dfrac{1}{9 } {AC}^{2} + \dfrac{1}{9} {BC}^{2} ) = 5 {OC}^{2}$