Предмет: Геометрия
Автор: Аноним
Вопрос задан 1 год назад

Точка Т – середина отрезка МР. Найдите координаты точки Р, если Т ( -2;4 ) и М ( -6;-7).

Ответы

Ответ дал: Аноним

171

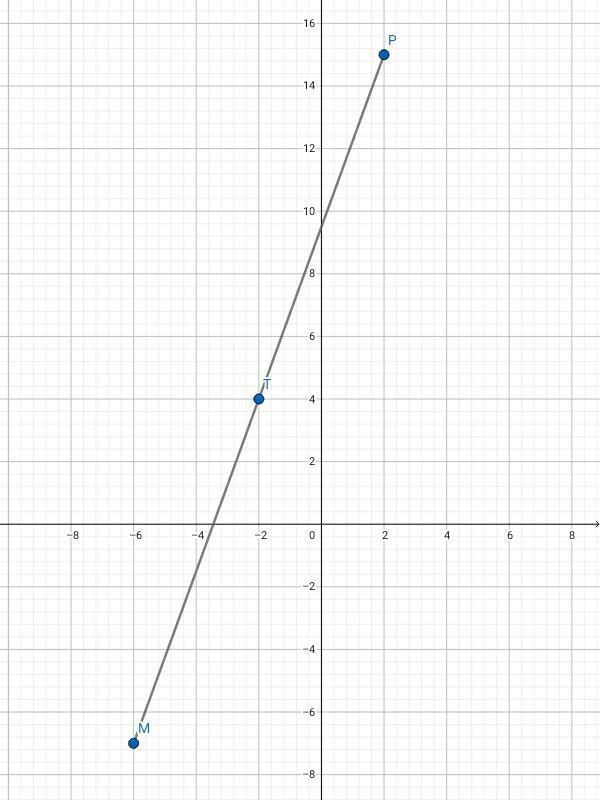
1. Составим уравнение для точки "T" по оси абсцисс и по оси ординат.

$T_{(x)}=\dfrac{M_{(x)}+P_{(x)}}{2} \\ \\ T_{(y)}=\dfrac{M_{(y)}+P_{(y)}}{2}$

2. Соответственно, чтобы найти координаты точки "P", нужно координаты точки "T" умножить на "2" и вычесть из произведения координаты точки "M".

$P_{(x)}=2\cdot T_{(x)} -M_{(x)}=2\cdot(-2)-(-6)=-4+6=\underline{2} \\ \\ P_{(y)}=2\cdot T_{(y)} -M_{(y)}=2\cdot4-(-7)=8+7=\underline{15}$

Ответ: P₍ₓ₎=2; P₍ᵧ₎=15.

Приложения:

Аноним: лайк у кого сейчас тоже сор

Kolyan7548: да ну у меня тоже сор

JagerTankist: Хех тоже сор

Аноним: Приветсвую Вас, участники многопользовательского сервиса "Школьные Знания"! Очень здорово, что приведённый выше ответ Вам помог, но убедительная просьба не посвящать данные комментарии общению. Они выделены для обсуждений данного ответа/вопроса. Все интересующие Вас вопросы не по теме этой страницы комментируйте, пожалуйста, в ЛС. Надеюсь на Ваше понимание! С Уважением, Маргарита.

Аноним: ок

Похожие вопросы

Русский язык

1 год назад

помогите пожалуйста найти члены предложения

Математика

1 год назад

помогите пожлуйста сделать

Английский язык

1 год назад

Напиши в минулому часі 1. She (to sleep) after dinner. 2. She (to get) up at seven o'clock. 3. She (to go) to bed at 11 p. m.

Английский язык