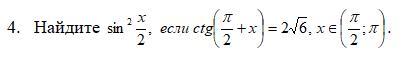Найдите $sin^{2}frac{x}{2}$ , если $ctg(frac{pi}{2}+x)=2sqrt{6} , xin(frac{pi }{2};pi ).$

Приложения:

Ответы

Ответ дал: Artem112

По формуле приведения получим:

$mathrm{ctg}left(dfrac{pi}{2}+xright)=-mathrm{tg}x=2sqrt{6}$

$mathrm{tg}x=-2sqrt{6}$

Выразим косинус через тангенс:

$1+mathrm{tg}^2x=dfrac{1}{cos^2x}$

$cos^2x=dfrac{1}{1+mathrm{tg}^2x}$

Так как косинус во второй четверти отрицателен, то:

$cos x=-sqrt{dfrac{1}{1+mathrm{tg}^2x} }$

Выразим искомое выражение:

$sin^2dfrac{x}{2} =dfrac{1-cos x}{2} =dfrac{1+sqrt{dfrac{1}{1+mathrm{tg}^2x} }}{2}$

$sin^2dfrac{x}{2} =dfrac{1+sqrt{dfrac{1}{1+(-2sqrt{6})^2} }}{2}=dfrac{1+sqrt{dfrac{1}{1+24} }}{2}=dfrac{1+dfrac{1}{5}}{2}=dfrac{3}{5}$

Похожие вопросы

Английский язык

1 год назад

Английский язык

1 год назад

Физика

2 года назад

Химия

2 года назад

Математика

8 лет назад

Геометрия

8 лет назад

Математика

9 лет назад

История

9 лет назад