Предмет: Алгебра
Автор: Goodbay
Вопрос задан 10 лет назад

< >

решить уравнения:

1. 2cos23x - cos3x=0

2. cos(х/2-1)=cos2(1-х/2)

3. sin23x + sinx + cos23x = 0

Приложения:

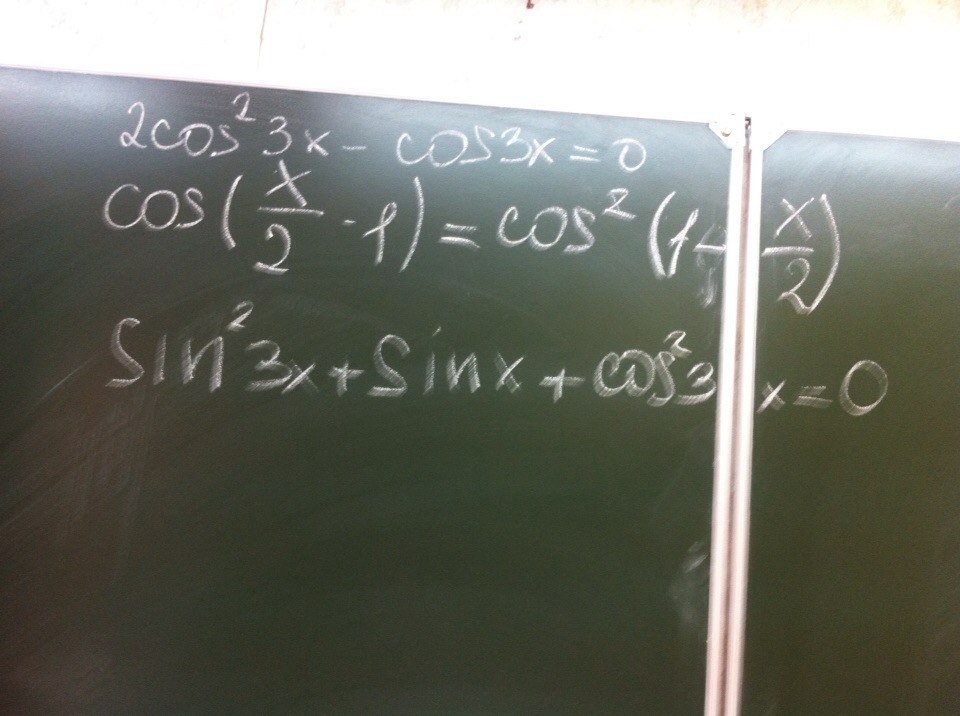
Ответы

Ответ дал: Аноним

0

$1) 2cos^23x-cos3x=0$
$cos3x(2cos3x-1)=0$
$cos3x=0$
$3x=frac{ pi }2+ pi n;neZ$
$x=frac{ pi }6+frac{ pi n}3;neZ$
$cos3x=frac{1}2$
$3x=frac{ pi }3+2 pi n;neZ$
$x=frac{ pi }9+frac{2 pi n}3;neZ$
$2)cos(frac{x}2-1)-cos^2(1-frac{x}2)=0$
$cos^2(frac{x}2-1)-cos(frac{x}2-1)=0$
$cos(frac{x}2-1)(cos(frac{x}2-1)-1)=0$
$cos(frac{x}2-1)=0$
$frac{x}2-1=frac{ pi }2+pi n;neZ$
$x= pi +2(1+ pi n);neZ$
$cos(frac{x}2-1)=1$
$frac{x}2-1=2 pi n;neZ$
$x=2(1+2 pi n);neZ$
$3)sin^23x+sinx+cos^23x=0$
$sinx=-1$
$x=-frac{ pi }2+2 pi n;neZ$

Приложения:

Похожие вопросы

Русский язык

2 года назад

Подскажите плиз спряжение глаголов Молить, Бормотать, Смотреть Заранее спасибо!

Русский язык

2 года назад

В слове ЖИЛКА есть беглый гласный?если да как доказать

Алгебра

7 лет назад

решить графически 0,5x²=2x-2

Математика

7 лет назад

(4x-5)0,6-0,3(4x-8)-(-1,6+1,2x)=1 Решите пожааалуйста

История

10 лет назад

какие изменения в сельском хоз произошли при петре1

Обществознание

10 лет назад

помогите привести примеры воспитания детей в разных странах

Геометрия

10 лет назад

помогите плиз!!! Сторона АВ треугольника АВС равна 1. Противолежащий ей угол С равен 30 градусам. Найти радиус окружности, около этого треугольника.

Алгебра

10 лет назад

Определить знак выражения sin125°×cos275°/tg295°×ctq175°