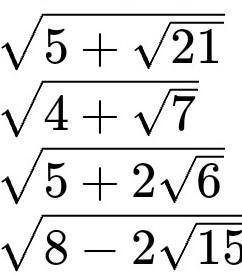Ответы
Ответ дал:
0
Ответ дал:
0
квадрат суммы и квадрат разности
Ответ дал:
0
упростите выражения
√(5 +√21 ) = √(10 +2√(7*3) ) /√2 =√( (√7)² +2√7*√3+(√(3)² ) / √2 =
=√( ( √7 +√3 )² ) / √2 = (√7 +√3 ) / √2 = 0,5 ( √14 +√6 ) .
- - -
√(4 +√7 ) = √(8 +2√(7*1) ) /√2 = √( (√7)² +2√7*1+1² ) / √2 =
=√( ( √7 +1 )² ) / √2 = (√7 +1 ) / √2 = 0,5 ( √14 +√2 ) .
- - -
√(5 +2√6 ) = √(3 +2√(3*2) +2 ) = √( (√3)² +2√3*√2+(√2)² ) =
=√( ( √3 +√2 )² ) = √3 +√2 .
- - -
√(8 -2√15 ) = √(5 - 2√(5*3) +3 ) = √( (√5)² - 2√5*√3+(√3) ² ) =
=√( ( √5 - √3 )² ) = √5 - √3 .
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад