Надо вычислить периметр и площадь трапеции.

Ответ:

P=5+5+10+5=20+5 cм

S=*BA===37,5

Пошаговое объяснение:

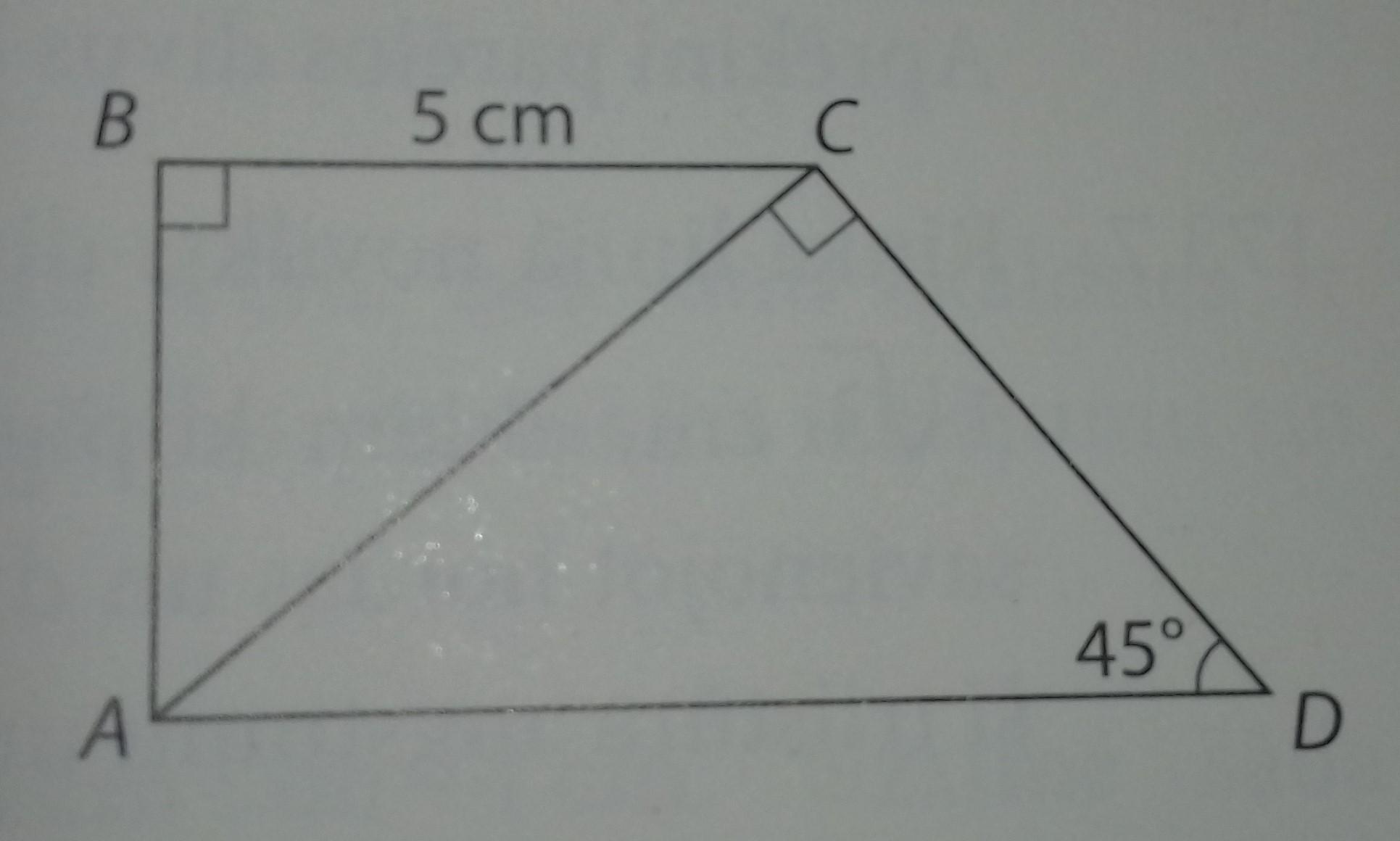
Проводимо відрізок СК. ∠DCK = 45° тоді KD=СK. BC=AK бо ABCK прямокутник. ∠ACK=45° тому AK=CK=5см. KD=5см AK= 10см. ∠ВСА=45° АВ=ВС=5см. CD==5.

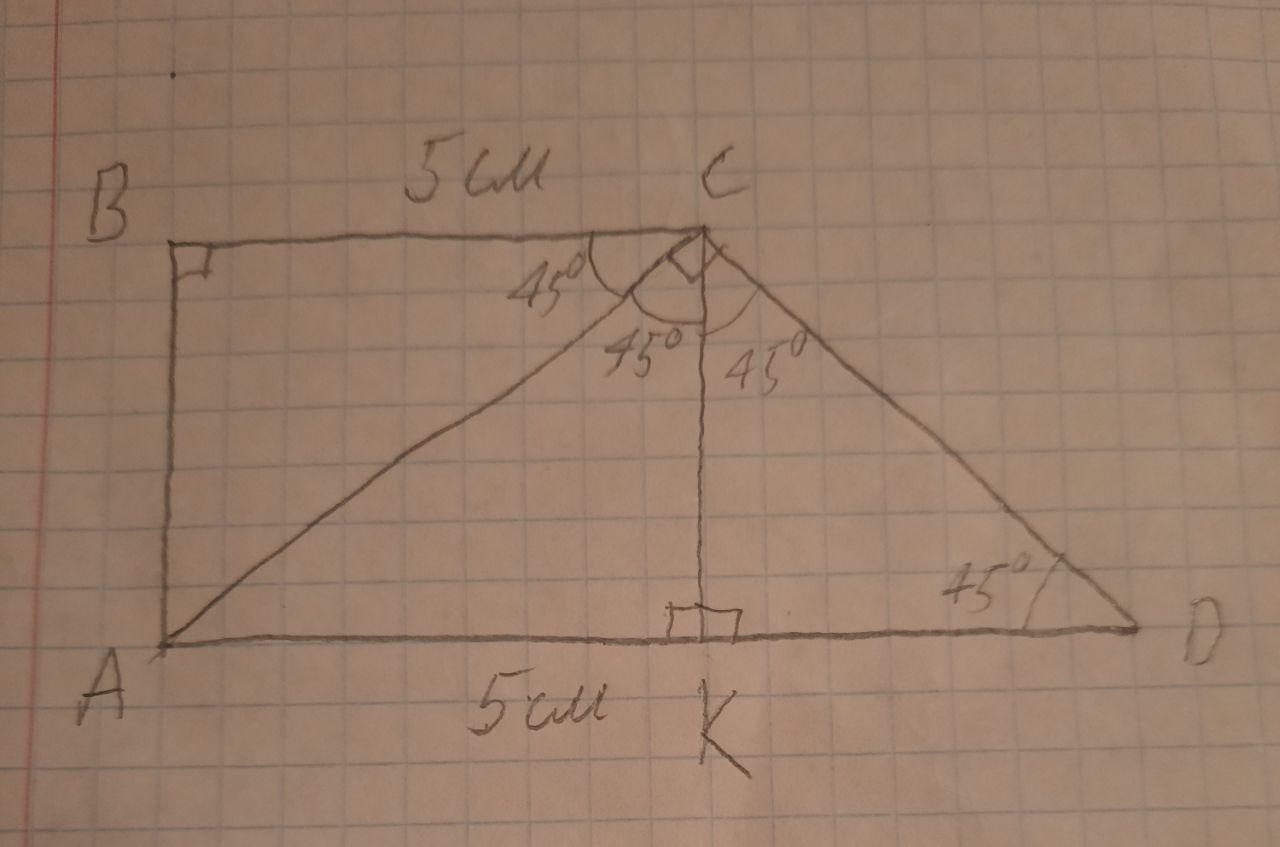
1) Рассмотрим треугольник АСД - прямоугольный (<АСД=90).

Т.к. <СДА=45, то по теореме о сумме углов треугольника <CАД=45. Следовательно, треугольник АСД - равнобедренный с основанием АД, а значит АС=СД.

2) <ВСА=<САД=45 (внутренние накрест лежащие углы при параллельных прямых АД и ВС - основания трапеции и секущей АС).

3) Рассмотрим треугольник АВС - прямоугольный (<АВС=90).

Т.к. <ВСА=45, то по теореме о сумме углов треугольника <САВ=45, т.е. треугольник АВС - равнобедренный с основанием АС, а значит АВ=ВС=5 см.

По теореме Пифагора

4) Из треугольника АСД по теореме Пифагора найдем АД:

6) Трапеция АВСД - прямоугольная. АВ - высота трапеции, а значит

Ответ: 20+5√2; 37,5