Ответы
Ответ дал:
0
Ответ:
вот
Пошаговое объяснение:
отметь как лучший пж
Приложения:
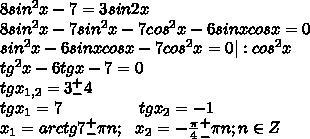
Ответ дал:
0
8t^2 - 7 = 3t;
8t^2 - 3t - 7 = 0;
t12 = (3 +- √9 - 4 * 8 * (-7)) / 2 * 8 = (3 +- 15) / 16;
t1 = (3 - 15) / 16 = -3/4; t2 = (3 + 15) / 16 = 9/8 - данный корень не удовлетворяет области определения функции y = sin(x).
Произведя обратную замену получим:
sin(x) = -3/4;
x = arcsin(-3/4) +- 2 * π * n, где n - натуральное число.
8t^2 - 3t - 7 = 0;
t12 = (3 +- √9 - 4 * 8 * (-7)) / 2 * 8 = (3 +- 15) / 16;
t1 = (3 - 15) / 16 = -3/4; t2 = (3 + 15) / 16 = 9/8 - данный корень не удовлетворяет области определения функции y = sin(x).
Произведя обратную замену получим:
sin(x) = -3/4;
x = arcsin(-3/4) +- 2 * π * n, где n - натуральное число.
Ответ дал:
0
в ответе должно получиться ±пи n; arctg+ пи k
Ответ дал:
0
Ответ:3sin2x - 8 sin^2x =7
3*2sincosx - 8 sin^2x - 7 sin^2x - 7 cos^2x = 0
6sinxcosx - 15sin^2x - 7cos^2x = 0 /:(-1)
15sin^2x - 6sinxcosx + 7cos^2x = 0 /:cos^2x≠0
15tg^2x - 6tgx + 7 = 0
tgx = t
15t^2 - 6t + 7 = 0
D = 36 - 4*15*7 < 0
Пошаговое объяснение:
Приложения:
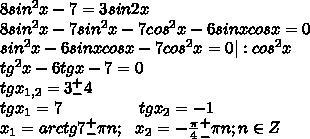
Похожие вопросы
1 год назад
1 год назад
2 года назад
8 лет назад
8 лет назад
9 лет назад