Помогите, очень срочно!!!
Завтра сдавать, а у меня нет решения :( пнкт не жалею!

1. Найти значение производной функции f(x)=2x^3+3x^2-x в точке х=-2.
2. Найти производную функции:
1) 2/x +4sqrt{х} - e^x 2)(3x-5)^3
3) 3sin2x*cosx 4) (x^3)/(x^2+5)
3. Найти угол между касательной к графику функции y=x^4-2x^3+3 в точке с абсциссой х0=1/2 и осью Ох.
4. Найти значения х, при которых значения функции f(x)=ln(3x+1) отрицательны.
5.Напишите уравнение касательной к графику функции y=1/3 x^3 - x^2 +5 которая параллельна прямой y=3x-2.

Ответы

Ответ дал: wejde

Все , что смогла.............................

Приложения:

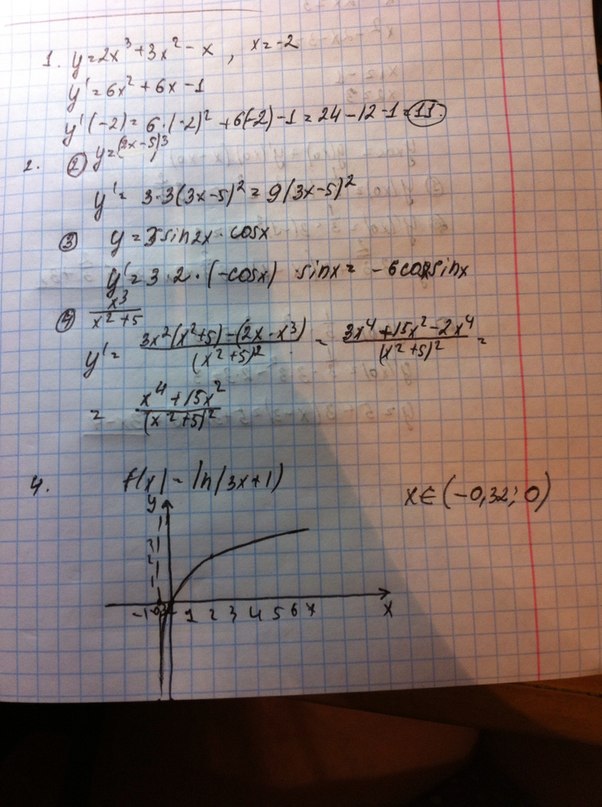
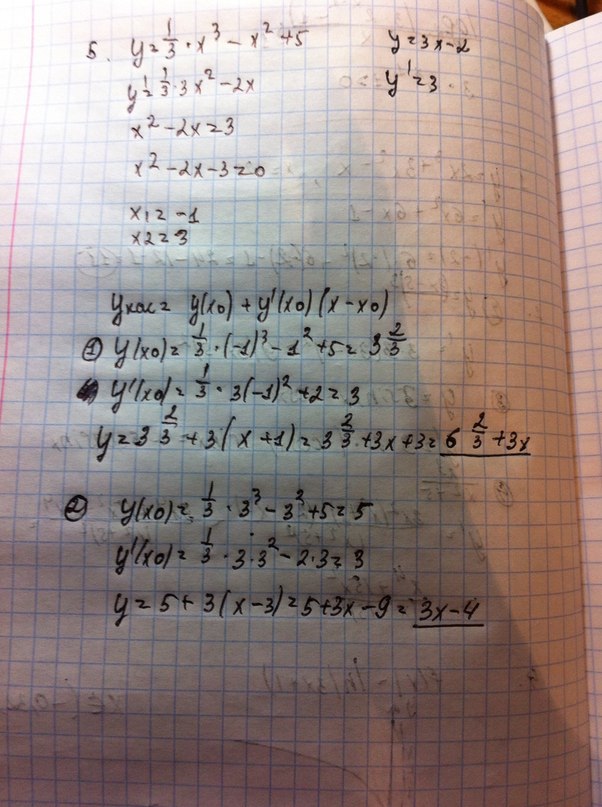
Ответ дал: SparDa9518

1. $6*x^2+6*x-1$ производная
$6*(-2)^2+6*(-2)-1=11$
2.
1) $- frac{2}{x^2} - frac{2}{ sqrt{x} } -e^x$
2) $3*(3*x-5)^2*3=9*(3*x-5)^2$
3) $6*cos(2x)*cos(x)+3*sin(2x)*sin(x)$
4) $frac{2*x^2*(x^2+5)-x^3*2*x}{(x^2+5)^2}$
3. $4*x^3-6*x^2$ производная
$y(1/2)= 4*(1/2)^3-6*(1/2)^2=-1$
4. По графику, от нуля до точки разрыва х = -0.32
5. $x^2-2*x=3$ производную функции приравниваем к 3, т.к угловой коэффициент прямой y=3*x-2 равен 3. Дальше находим значение x и его подставляем в исходное уравнение y=1/3*x^3-x^2+5 получаем y=5,
Искомое уравнение принимает вид y=k*x+b, b=-4 (подставив значение y=5 x=3)
Искомое уравнение имеет вид y=3*x-4

Приложения:

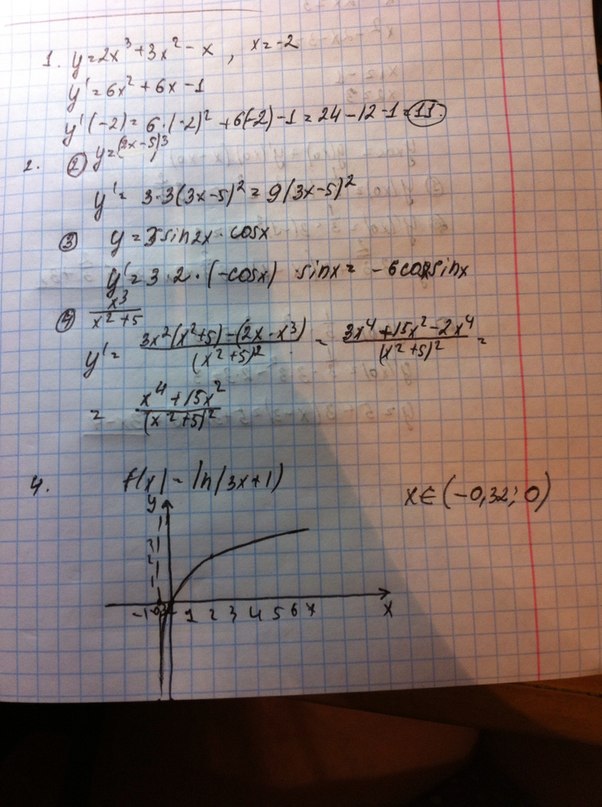
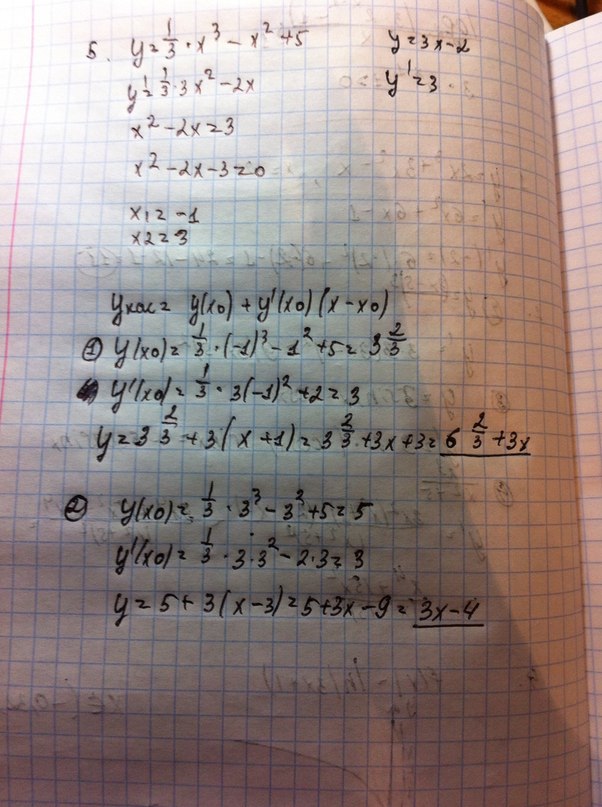
Похожие вопросы

Русский язык

2 года назад

любое предложение со словами написать,сделать

Русский язык

2 года назад

Вставьте пропущенные буквы. В глаголах обозначьте суффиксы. Из данных словосочетаний выпишите только те, в которых глаголы используются в прямом значении.Завяз.....вать знакомство, завязывать

Алгебра

7 лет назад

точка пересечения с осью ОХ y=5-x^3+3x^2

Математика