Образующая конуса наклонена к плоскости основания под углом 60 градусов и равна 6см Найдите площадь осевого сечения конуса. (Должен получится ответ 9 м^2)

Ответ:

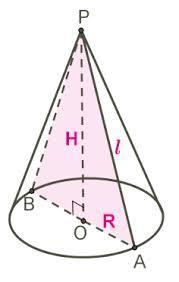
Пошаговое объяснение: Дано: ∠РАО=60°,  l=РА=6 cм. Δ РВА -осевое сечение.  Найти S  (площадь Δ РВА)               Решение:   Δ РВА - равнобедренный, т.к. РВ=РА как образующие конуса, ⇒углы при основании равны, т.е ∠РВА=∠РАв=60°, знаит угол при вершине ∠Р=180°-(60°+60°)=60° ⇒     Δ РВА -правильный, ⇒S=PA·PB·Sin60°= 6·6·√3/2 = 18√3 (см²)        Замечание: И это правильный ответ!!!