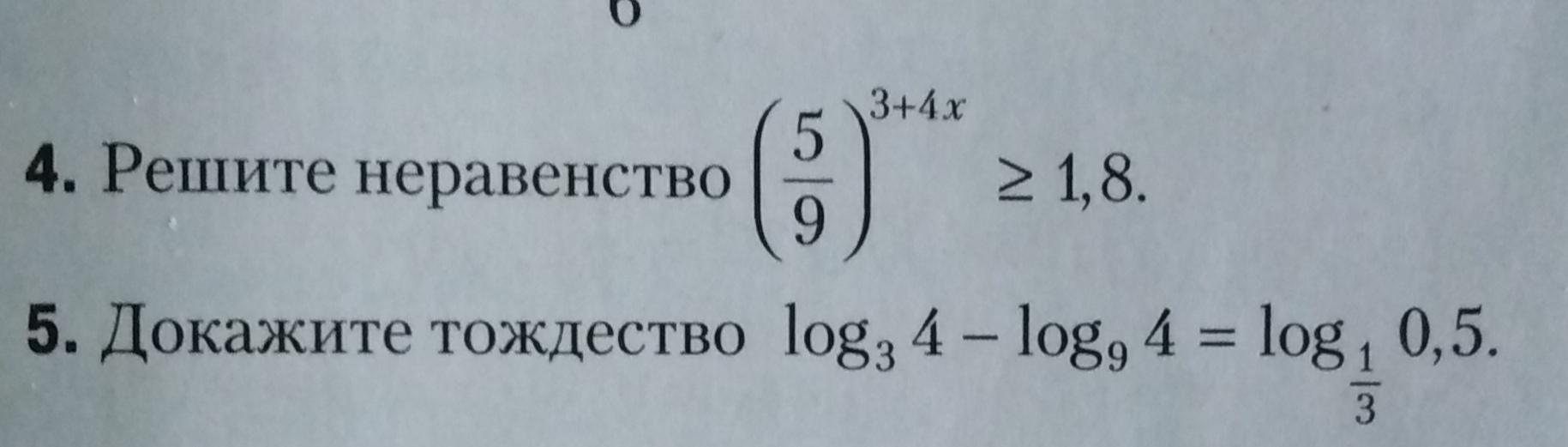Предмет: Алгебра
Автор: ilya6240
Вопрос задан 7 лет назад

< >

ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ 2 УРАВНЕНИЯ!!! ДАМ БАЛЛЫ

Приложения:

Ответы

Ответ дал: ipetrovxx85

0

Решить неравенство:

$left(frac{5}{9} right)^{3+4x}geq 1,8\\| : 1,8 = 1frac{8}{10} =1frac{4}{5} = frac{9}{5} =frac{5}{9}^{-1} \\left(frac{5}{9} right)^{3+4x}geq frac{5}{9}^{-1} \\3+4xle -1\\4xle -4\\xle -1$

Ответ: x ∈ (−∞; -1].

Доказать тождество:

$log_{3}(4)-log_{9}(4)=log_{frac{1}{3}} (0,5)\\log_3left(2^2right)-log_{3^2}left(2^2right)=log_{3^-1}left(2^{-1}right)\\2log_3left(2right)-frac{2}{2} log_{3}left(2right)=frac{-1}{-1} log_{3}left(2}right)\\2log_3left(2right)-log_3left(2right)=log_3left(2right)\\log_3left(2right)=log_3left(2right)$

Тождество доказано.

Похожие вопросы

Математика

2 года назад

теплоход прошел по реке расстояние междк двумя пристанями,равное 80 км, за 3 часа 20 минут по течению реки и за 5 часов против течения.Найти скорость течения реки и собственную скорость теплохода

Окружающий мир

2 года назад

Как определить по черепу чей он?

Қазақ тiлi

2 года назад

Андронов тайпаларының үлкен қоныстары неше үйден тұратын болған:

Биология

2 года назад

Прочитайте текст местные экосистемы .Определите из предложенного текста экологические факторы абиотические биотические и антропогенные

Химия

8 лет назад

Вычислить объем кислорода и азота которые можно получить из 1000м3 воздуха Содержание в воздухе кислорода 21% а азота -78% по объёму

Геометрия

8 лет назад

Угол между биссектрисой данного угла и лучом дополнительным к одной из его сторон, равен 126 градусов. Найдите данный угол

Математика

9 лет назад

РЕШИТЬ УРАВНЕНИЯ (3Х+2)^2-9Х^2=0

Математика

9 лет назад

Пять девятых перевести в смешанную дробь