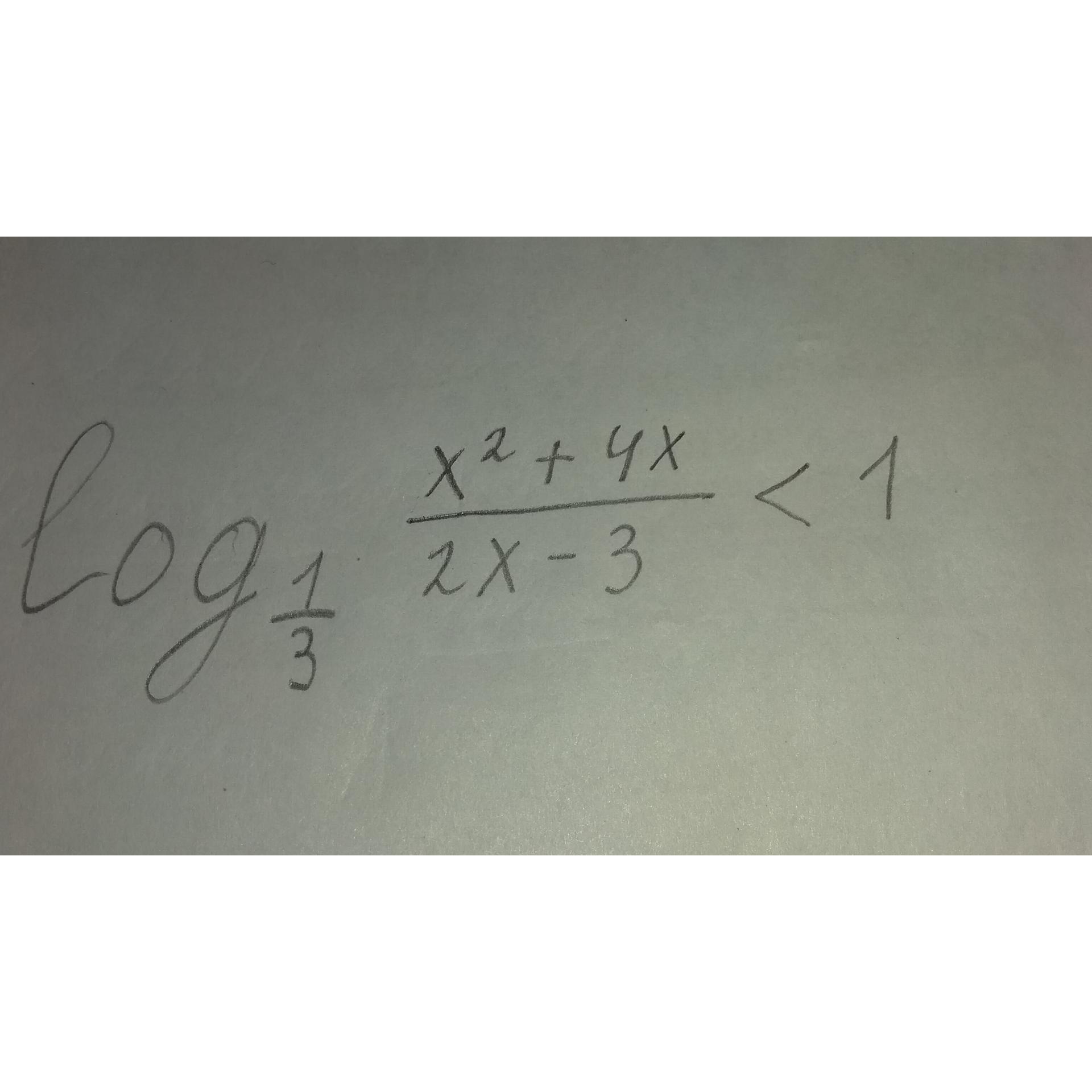Предмет: Алгебра
Автор: servas444444
Вопрос задан 1 год назад

< >

Решить неравенство Помогите ,буду благодарен.

Приложения:

Ответы

Ответ дал: sangers1959

1

Ответ:

Объяснение:

ОДЗ:

$\frac{x^{2}+4x }{2x-3} >0\\\frac{x*(x+4)}{2x-3}>0$

-∞__-__-4__+__0__-__1,5__+__+∞

x∈(-4;0)U(1,5;+∞).

$log_{\frac{1}{3} } \frac{x^{2} +4x}{2x-3} <1\\ \frac{x^{2} +4x}{2x-3}>\frac{1}{3}\\ \frac{x^{2} +4x}{2x-3}-\frac{1}{3} >0\\\frac{3*(x^{2}+4x)-2x+3 }{3*(2x-3)} >0\\\frac{3x^{2}+12x-2x+3 }{3*(2x-3)} >0\\\frac{3x^{2} +10x+3}{3*(2x-3)}>0|*3\\ \frac{3x^{2}+9x+x+3 }{2x-3}>0\\\frac{3x*(x+3)+(x+3)}{2x-3} >0\\\frac{(x+3)*(3x+1)}{2x-3} >0$

-∞__-__-3__+__-1/3__-__1,5__+__+∞

x∈(-3;-1/3)U(1,5;+∞)

Согласно ОДЗ:

Ответ: x∈(-3;-1/3)U(1,5;+∞).

Похожие вопросы

Геометрия

1 год назад

Дано: ΔABE = ΔCDE AB = 12 см AE = 8 см CE = 6см Знайти: CD

Математика

1 год назад

помогите пожалуйста фото прикрепил

Литература

1 год назад

опрацювати матеріал підручника, стр.184-189, ознайомитися з цією презентацією; письмово у зошиті відповісти на питання: 1. Реалізм – це… 2. Основні риси реалізма: 3. Вказати найвідоміших

Физика

1 год назад

який об'єм газу при температурі 27 що створює тиск 2000 якщо кількість молей газу 5моль

Химия

2 года назад

1. Чому алкени виявляють більшу хімічну активність, ніж алкани та циклоалкани? 2. Допишіть речення. найхарактернішими реакціями алкенів є реакції приєднання __________, повного __________,

Қазақ тiлi

2 года назад

ана-тілі мақтанышым эссе 150 сөз Пожалуйста помогите мне СРОЧНО нужен эссе Потом я вам помогу

Математика

8 лет назад

как решаются задачи когда известен результат разностного сравнения

Математика

8 лет назад

найдите объем параллелепипеда