Помогите пожалуйста, желательно с Дано, Доказать и Доказательством.​

Дано:

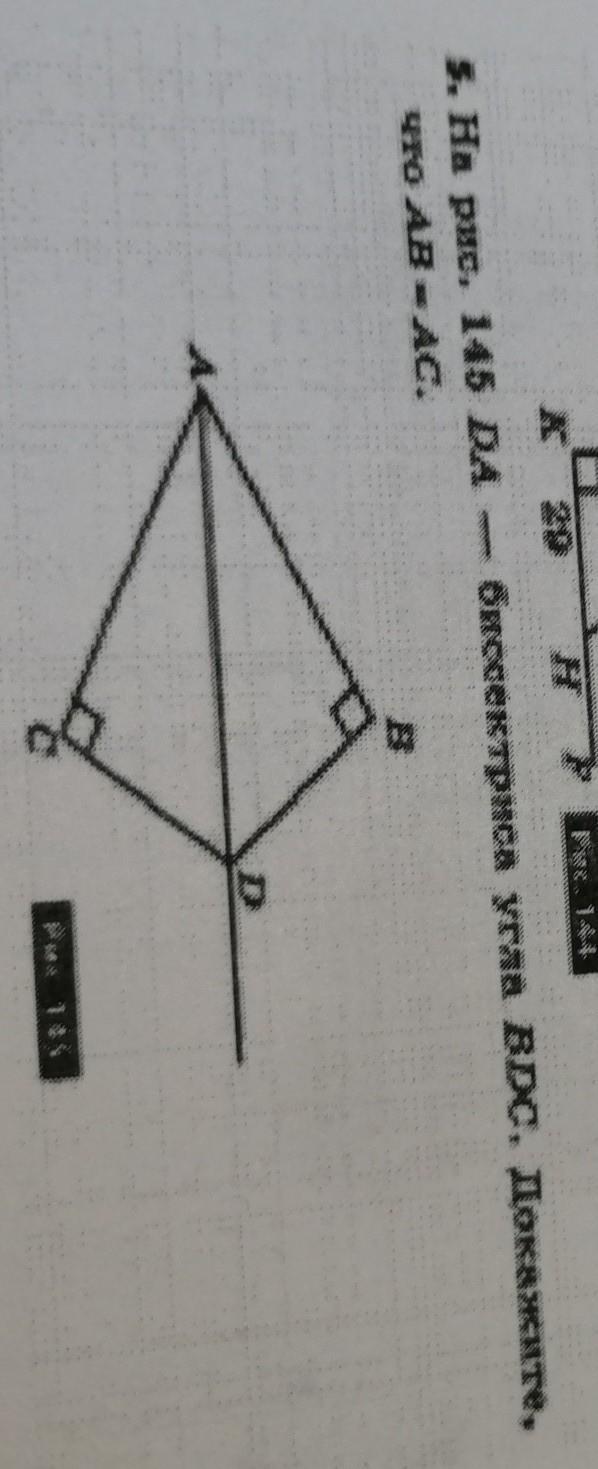
∆ACD и ∆ABD - прямоугольные.

AD - биссектриса.

Доказать:

АВ = АС

Решение.

AD - общая сторона.

Так как АD - биссектриса => ∠CDA = ∠BDA.

=> ∆ACD = ∆ABD, по гипотенузе и острому углу.

=> АВ = АС.

Ч.Т.Д.

Ответ:

дано

треугольник ABD b ACD

угол B=90 b угол C=90 градусов

доказать AB=AC

доказательство

AD-общая

угол CAD=углу BAD т,к AD бессектриса

угол ADC=ADB т,к AD бессектриса

треугольник ADB=треугольнику ACD по 2 признаку

=> AC=AB

Объяснение: