Из одной точки окружности проведены две взаимно перпендикулярные хорды, длины которых равны 8 и 15. На какое расстоянии от центра окружности удалена большая хорда?
помогите пожалуйста , нужно очень срочно
Ответы
Ответ дал:
1
Ответ:
Расстояние от центра окружности до большей хорды равно 4.
Объяснение:
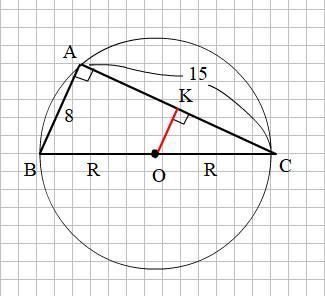
Смотри прикреплённый рисунок
Поскольку хорды АВ и АС образуют прямой вписанный угол ВАС, который опирается на диаметр ВС.
Центр окружности О делит гипотенузу ВС треугольника АВС пополам,
Поэтому перпендикуляр ОК, опущенный из точки О на большую хорду АС, параллелен стороне АВ и является средней линией.
Средняя линия треугольника равна половине стороны, которой она параллельна, поэтому ОК = 0,5 АВ = 0,5 · 8 = 4
Приложения:
Похожие вопросы
1 год назад
1 год назад
8 лет назад