log5(x^2-7x+6 )< log5(x-6)

log₅(x²-7x+6) < log₅(x-6)

f(x) = log₅x - возрастающая функция

Поэтому x²-7x+6 < x-6 при условии, что x²-7x+6>0, поскольку это аргумент логарифма. Условие на x-6 нет смысла накладывать т.к. оно уже больше неотрицательного выражения.

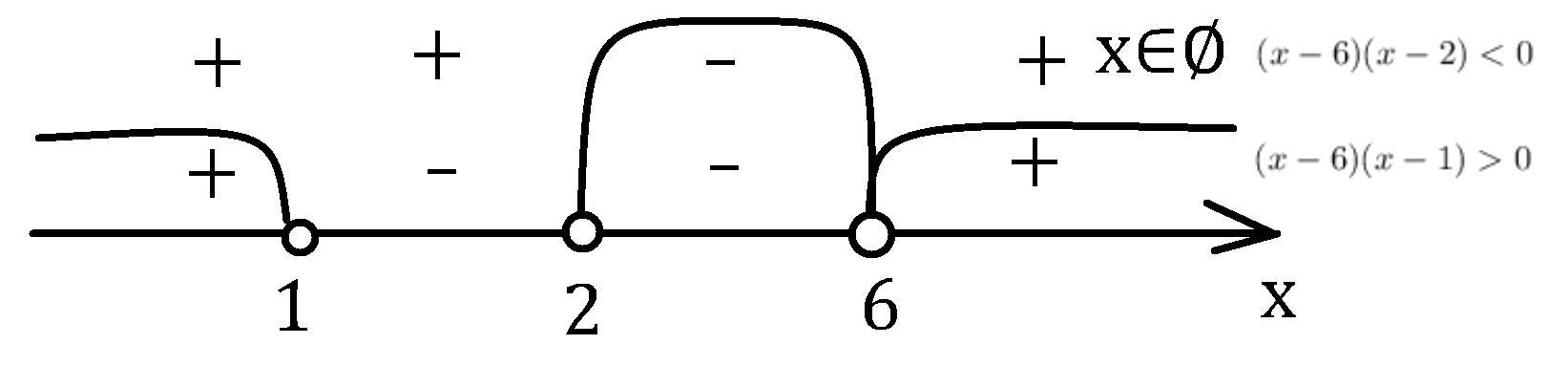
Решим систему на координатной прямой.

Ответ: x∈∅. Нет решений.